
椭圆E的中心在坐标原点O,焦点在x轴上,离心率为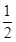 ,点P(1,
,点P(1,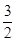 )和A、B都在椭圆E上,且
)和A、B都在椭圆E上,且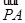 +
+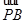 =m
=m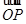 (m∈R).
(m∈R).
(1)求椭圆E的方程及直线AB的斜率;
(2)当m=-3时,证明原点O是△PAB的重心,并求直线AB的方程.
(1)由 =
=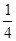 及
及 解得a2=4,b2=3,
椭圆方程为
解得a2=4,b2=3,
椭圆方程为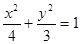 ;……2分
;……2分
设A(x1,y1)、B(x2,y2), 由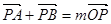 得
得
(x1+x2-2,y1+y2-3)=m(1,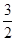 ),即
),即
又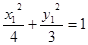 ,
,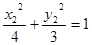 ,两式相减得
,两式相减得
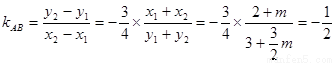 ; ………………………6分
; ………………………6分
(2)由(1)知,点A(x1,y1)、B(x2,y2)的坐标满足 ,
,
点P的坐标为(1,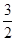 ), m=-3, 于是x1+x2+1=3+m=0,y1+y2+
), m=-3, 于是x1+x2+1=3+m=0,y1+y2+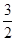 =3+
=3+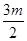 +
+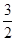 =0,
=0,
因此△PAB的重心坐标为(0,0).即原点是△PAB的重心.
∵x1+x2=-1,y1+y2=-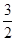 ,∴AB中点坐标为(
,∴AB中点坐标为(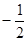 ,
,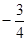 ),………………………10分
),………………………10分
又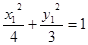 ,
,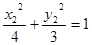 ,两式相减得
,两式相减得
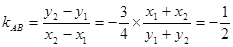 ;
;
∴直线AB的方程为y+ =
=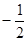 (x+
(x+ ),即x+2y+2=0.
),即x+2y+2=0.
【解析】(1)由椭圆上的点P,及离心率可以建立关于a,b,c的两个方程,再根据a2=b2+c2,解方程组即可。根据 +
+ =m
=m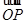 ,然后坐标化即可用m表示出x1+x2,y1+y2,然后把A、B坐标代入椭圆方程,作差即可求出AB的斜率。
,然后坐标化即可用m表示出x1+x2,y1+y2,然后把A、B坐标代入椭圆方程,作差即可求出AB的斜率。
(2)在第(1)问的基础上根据重心坐标公式即可求解。


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
| ||
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
| PA |
| PB |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
| PA |
| PB |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com