
如图,已知三棱柱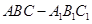 的侧棱与底面垂直,
的侧棱与底面垂直,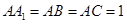 ,
,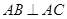 ,
,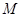 ,
,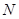 分别是
分别是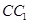 ,
,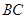 的中点,点
的中点,点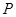 在直线
在直线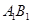 上,且
上,且 ;
;
(Ⅰ)证明:无论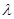 取何值,总有
取何值,总有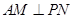 ;
;
(Ⅱ)当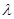 取何值时,直线
取何值时,直线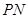 与平面
与平面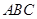 所成的角
所成的角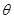 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;
(Ⅲ)是否存在点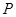 ,使得平面
,使得平面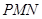 与平面
与平面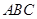 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点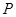 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.

(1)略
(2)∴当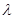 =
=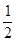 时,θ取得最大值,此时sinθ=
时,θ取得最大值,此时sinθ=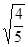 ,cosθ=
,cosθ=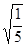 ,tanθ=2
,tanθ=2
(3)∴不存在点P使得平面PMN与平面ABC所成的二面角为30º
【解析】本题主要考查了直线与平面所成的角,以及直线与平面垂直的性质,考查空间想象能力,属于基础题.
(1)以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz,分别求出 PN,AM
的坐标,要证PN⊥AM,只需求证它们的数量积为零即可;
(2)过P作PE⊥AB于E,连接EN,则∠PNE为直线PN与平面ABC所成的角θ,求出此角的正切值,然后研究其最大值即可求出λ的值.
(3) 假设存在,则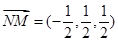 ,设
,设 是平面PMN的一个法向量,那么利用向量的坐标得到参数
是平面PMN的一个法向量,那么利用向量的坐标得到参数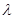 的值,进而判定方程有无解,说明结论。
的值,进而判定方程有无解,说明结论。


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源:2014届山东省济宁市高二10月月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,已知三棱柱 的侧棱与底面垂直,
的侧棱与底面垂直, ,
,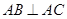 ,
, ,
, 分别是
分别是 ,
,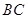 的中点,点
的中点,点 在直线
在直线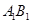 上,且
上,且 ;
;
(1)证明:无论 取何值,总有
取何值,总有 ;
;
(2)当 取何值时,直线
取何值时,直线 与平面
与平面 所成的角
所成的角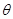 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;
(3)是否存在点 ,使得平面
,使得平面 与平面
与平面 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2013届江苏无锡市高二第二学期期中数学理试卷(解析版) 题型:解答题
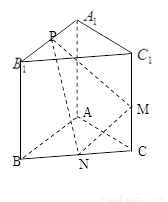
如图,已知三棱柱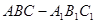 的侧棱与底面垂直,
的侧棱与底面垂直,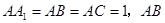 ⊥AC,M是
⊥AC,M是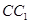 的中点,N是BC的中点,点P在直线
的中点,N是BC的中点,点P在直线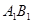 上,且满足
上,且满足 .
.
(1)当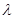 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角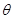 最大?
最大?
(2)若平面PMN与平面ABC所成的二面角为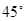 ,试确定点P的位置.
,试确定点P的位置.
查看答案和解析>>
科目:高中数学 来源:2012届湖北省高二下学期期中考试理科数学卷 题型:解答题
如图,已知三棱柱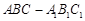 的侧棱与底面垂直,
的侧棱与底面垂直,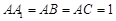 ,
,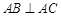 ,M是
,M是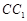 的中点,
的中点,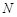 是
是 的中点,点
的中点,点 在
在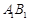 上,且满足
上,且满足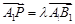 .
.
(1)证明: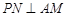 .
.
(2)当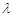 取何值时,直线
取何值时,直线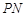 与平面
与平面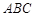 所成的角
所成的角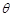 最大?并求该角最大值的正切值.
最大?并求该角最大值的正切值.
(3)若平面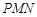 与平面
与平面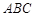 所成的二面角为
所成的二面角为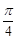 ,试确定P点的位置.
,试确定P点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知三棱柱![]() 的侧棱与底面垂直,
的侧棱与底面垂直,![]() ⊥AC,
⊥AC,
M是![]() 的中点,N是BC的中点,点P在直线
的中点,N是BC的中点,点P在直线![]() 上,且满足
上,且满足![]() .
.
(Ⅰ)当![]() 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角![]() 最大?并求sin
最大?并求sin![]() 的值;
的值;
 (Ⅱ)若平面PMN与平面ABC所成的二面角为
(Ⅱ)若平面PMN与平面ABC所成的二面角为![]() ,试确定点P的位置.
,试确定点P的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com