解:(1)
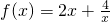
根据耐克函数的性质,
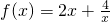
的单调递减区间是
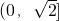
,证明如下:
设任意
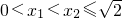
,
则
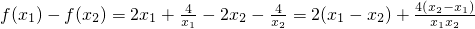
=
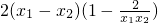
∵
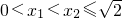
∴
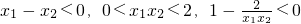
∴f(x
1)-f(x
2)>0
所以
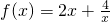
的单调递减区间是
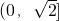
(2)∵
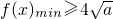
∴16a>b
4 基本事件总数为6×6=36,
当a=1时,b=1;
当a=2,3,4,5时,b=1,2,共2×4=8种情况;
当a=6时,b=1,2,3;
目标事件个数为1+8+3=12.因此所求概率为

.
分析:(1)利用函数单调性定义求单调区间,可先判断其单调性,再用定义证明,证明时需经过设、差、变、判、结五步解决;
(2)先由f(x)>b
2恒成立,可知f(x)的最小值大于b
2,可得a、b间的不等关系,再利用古典概型公式,用列举法得目标事件在基本事件总数中的比例即可
点评:本题综合考查了函数单调性的定义及证明方法,函数、不等式与概率的综合,解题时要认真体会函数问题是怎样与计数概率联系起来的

 .
.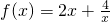
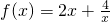 的单调递减区间是
的单调递减区间是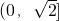 ,证明如下:
,证明如下: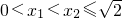 ,
,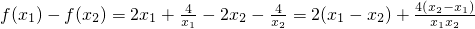 =
=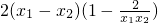
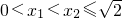 ∴
∴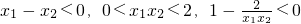
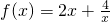 的单调递减区间是
的单调递减区间是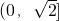
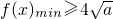
 .
.
