
 ,P1(x1,y1)、P2(x2,y2)是函数y=f(x)图象上两点,且线段P1P2中点P的横坐标是
,P1(x1,y1)、P2(x2,y2)是函数y=f(x)图象上两点,且线段P1P2中点P的横坐标是 .
.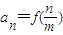 (m∈N*),n=1,2…m),求数列{an}的前m项和Sm;
(m∈N*),n=1,2…m),求数列{an}的前m项和Sm;  恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. 知,x1+x2=1,故y1+y2=
知,x1+x2=1,故y1+y2=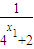 +
+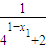 ,由此能够证明点P的纵坐标是定值.
,由此能够证明点P的纵坐标是定值.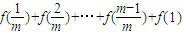 ,利用倒序相加法能够求出数列{an}的前m项和Sm.
,利用倒序相加法能够求出数列{an}的前m项和Sm.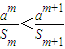 ,得12am(
,得12am( -
- )<0对m∈N+恒成立.由此利用分类讨论思想能够求出实数a的取值范围.
)<0对m∈N+恒成立.由此利用分类讨论思想能够求出实数a的取值范围. 知,x1+x2=1,则
知,x1+x2=1,则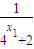 +
+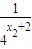
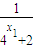 +
+
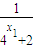 +
+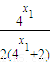
 ,
, ,为定值.
,为定值.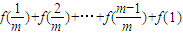 ,
,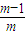 )+f(
)+f(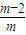 )+…+f(
)+…+f(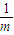 )+f(1)
)+f(1) +
+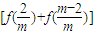 +…+
+…+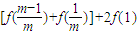 ,
, ,…m-1),故
,…m-1),故 ,
,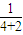 =
= ,从而
,从而 .(12分)
.(12分)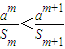 ,
,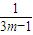 -
-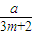 )<0…①对m∈N+恒成立.
)<0…①对m∈N+恒成立.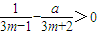 ,得am<0.
,得am<0.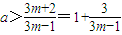 .
.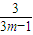 随m的增大而减小,
随m的增大而减小,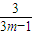 有最大值
有最大值 ,故a
,故a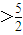 .(18分)
.(18分)

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:杨浦区一模 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com