
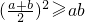 ,②
,②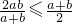 ,③
,③ ,④
,④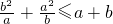 ;其中正确的个数是
;其中正确的个数是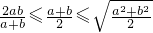 ”,即要证明两个不等式:“
”,即要证明两个不等式:“ ”对于前一个可直接利用作差法;对于后一个先将两边的式子平方后再利用作差的方法,作差后结合基本不等式进行证明即得.
”对于前一个可直接利用作差法;对于后一个先将两边的式子平方后再利用作差的方法,作差后结合基本不等式进行证明即得.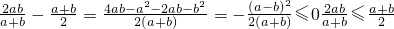 ,
,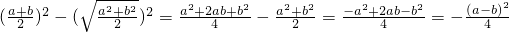
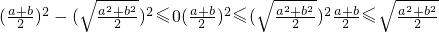 ,
,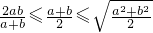 ,当且仅当a=b时等号成立;
,当且仅当a=b时等号成立;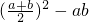 =
=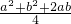 =
=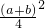 ≥0,成立,故 ①正确.
≥0,成立,故 ①正确.

科目:高中数学 来源: 题型:
| y2 |
| a2 |
| x2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MA |
| AN |
| MB |
| BN |
查看答案和解析>>
科目:高中数学 来源:2008年上海市上海中学高三3月综合练习数学试卷1(文理合卷)(解析版) 题型:解答题
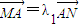 ,
,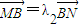 ,问λ1+λ2是否为定值?说明理由.
,问λ1+λ2是否为定值?说明理由.查看答案和解析>>
科目:高中数学 来源:2010年上海市上海中学高三数学综合练习试卷(1)(解析版) 题型:解答题
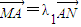 ,
,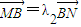 ,问λ1+λ2是否为定值?说明理由.
,问λ1+λ2是否为定值?说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com