
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,
大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,
当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:
当20≤x≤200时,车流速度v是车流密度x的一次函数.
(I) 当0≤x≤200时,求函数v(x)的表达式;
(II) 当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,
单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时).
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:专项题 题型:解答题
| 某商场在促销期间规定:商场内所有商品按标价的80%出售;同时当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券: | ||||||||||||
 。试问: 。试问: | ||||||||||||
| (1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少? (2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不小于 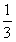 的优惠率? 的优惠率? |
查看答案和解析>>
科目:高中数学 来源:0113 期中题 题型:单选题
查看答案和解析>>
科目:高中数学 来源:河北省会考题 题型:单选题
[ ]
查看答案和解析>>
科目:高中数学 来源:同步题 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com