
甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)设 ,
,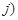 表示甲乙抽到的牌的数字,
表示甲乙抽到的牌的数字, 如甲抽到红桃2,乙抽到红桃3,记为
如甲抽到红桃2,乙抽到红桃3,记为 ,
,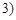 ,写出甲乙二人抽到的牌的所有情况;
,写出甲乙二人抽到的牌的所有情况;
(2)若甲抽到红桃3,则乙抽出的牌面数字比3大的概率是多少?
(3)甲乙约定,若甲抽到的牌的牌面数字比乙大,则甲胜;否则,乙胜,你认为此游戏是否公平?请说明理由.
(1)详见解析;(2)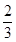 ;(3)不公平.
;(3)不公平.
解析试题分析:(1)此题为古典概型的概率计算问题,因为有两张4,所以在列举时,要做一区分,设方片4为4′,甲乙两人抽到的牌不放回,所以在甲抽完以后,乙只能从剩下的牌中抽取,然后一一列举出所以基本事件;(2)在(1)中列举的所以情况看,横坐标为3的有几个基本事件N,其中大于3的有几个基本事件n, ,就是甲抽到红桃3,则乙抽出的牌面数字比3大的概率;(3)同样在(1)中找到甲抽到的牌的牌面数字大于乙的基本事件,剩下的基本事件为乙大的,分别让他们除以总的基本事件,看谁的概率大,相等,即公平,不相等,就是不公平.
,就是甲抽到红桃3,则乙抽出的牌面数字比3大的概率;(3)同样在(1)中找到甲抽到的牌的牌面数字大于乙的基本事件,剩下的基本事件为乙大的,分别让他们除以总的基本事件,看谁的概率大,相等,即公平,不相等,就是不公平.
试题解析:(1)解:方片4用4′表示,则甲乙二人抽到的牌的所有情况为:
(2,3),(2,4),(2,4′),(3,2),(3,4),(3,4′),(4,2),(4,3),(4,4′),
(4′,2),(4′,3),(4′,4)共12种不同的情况. 5分
(2)解:甲抽到3,乙抽到的牌只能是2,4,4′,
因此乙抽到的牌的数字大于3的概率为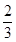 . 8分
. 8分
(3)解:甲抽到的牌比乙大,有(4,2),(4,3),(4′,2),(4′,3),(3,2)共5种
情况.
甲胜的概率为 ,乙胜的概率为
,乙胜的概率为 ,
,
因为 ,所以此游戏不公平. 13分
,所以此游戏不公平. 13分
考点:古典概型的概率计算


科目:高中数学 来源: 题型:解答题
中国共产党第十八次全国代表大会期间,某报刊媒体要选择两名记者去进行专题采访,现有记者编号分别为1,2,3,4,5的五名男记者和编号分别为6,7,8,9的四名女记者.要从这九名记者中一次随机选出两名,每名记者被选到的概率是相等的,用符号(x,y)表示事件“抽到的两名记者的编号分别为x、y,且x<y”.
(1)共有多少个基本事件?并列举出来;
(2)求所抽取的两名记者的编号之和小于17但不小于11或都是男记者的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表: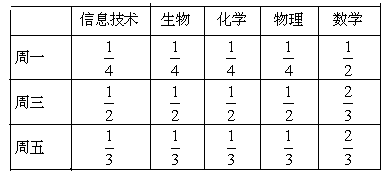
根据上表:
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为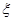 ,求随机变量
,求随机变量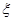 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次数学测验后,班级学委对选答题的选题情况进行了统计,如下表:
| | 几何证明选讲 | 坐标系与 参数方程 | 不等式选讲 | 合计 |
| 男同学(人数) | 12 | 4 | 6 | 22 |
| 女同学(人数) | 0 | 8 | 12 | 20 |
| 合计 | 12 | 12 | 18 | 42 |
| | 几何类 | 代数类 | 总计 |
| 男同学(人数) | 16 | 6 | 22 |
| 女同学(人数) | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和,求ξ的分布列;
(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)=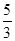 ,D(η)=
,D(η)=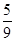 ,求a∶b∶c.
,求a∶b∶c.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为备战2016年奥运会,甲、乙两位射击选手进行了强化训练.现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次,记录如下:
甲:8.3,9.0,7.9,7.8,9.4,8.9,8.4,8.3;
乙:9.2,9.5,8.0,7.5,8.2,8.1,9.0,8.5.
(1)画出甲、乙两位选手成绩的茎叶图;
(2)现要从中选派一人参加奥运会封闭集训,从统计学角度,你认为派哪位选手参加合理?简单说明理由;
(3)若将频率视为概率,对选手乙在今后的三次比赛成绩进行预测,记这三次成绩中不低于8.5分的次数为ξ,求ξ的分布列及均值E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某牛奶厂要将一批牛奶用汽车从所在城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且运费由厂商承担.若厂商恰能在约定日期(×月×日)将牛奶送到,则城市乙的销售商一次性支付给牛奶厂20万元;若在约定日期前送到,每提前一天销售商将多支付给牛奶厂1万元;若在约定日期后送到,每迟到一天销售商将少支付给牛奶厂1万元.为保证牛奶新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送牛奶,已知下表内的信息:
| 统计信息 汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
| 公路1 | 2 | 3 | 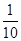 | 1.6 |
| 公路2 | 1 | 4 | 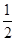 | 0.8 |
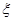 (单位:万元),求
(单位:万元),求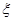 的分布列和数学期望
的分布列和数学期望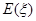 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求 的分布列及数学期望
的分布列及数学期望查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为贯彻“激情工作,快乐生活”的理念,某单位在工作之余举行趣味知识有奖竞赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为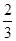 .
.
(1)求选手甲答题次数不超过4次可进入决赛的概率;
(2)设选手甲在初赛中答题的个数为X,试写出X的分布列,并求X的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com