
分析 (Ⅰ)求出函数的导数,计算f′(1),求出a的值即可;(Ⅱ)通过讨论x的范围,0得a>-$\frac{{x}^{2}}{2lnx}$,令g(x)=-$\frac{{x}^{2}}{2lnx}$(x>1),求出函数的单调区间,求出a的范围即可.
解答 解:(Ⅰ)f′(x)=2x+$\frac{2a}{x}$=$\frac{2{(x}^{2}+a)}{x}$,
由f′(1)=2+2a=0,解得:a=-1,
经检验a=-1时取极小值,
故a=-1;
(Ⅱ)由f(x)>0,即x2+2alnx>0,对任意x∈[1,+∞)恒成立,
(1)x=1时,有a∈R,
(2)x>1时,x2+2alnx>0得a>-$\frac{{x}^{2}}{2lnx}$,
令g(x)=-$\frac{{x}^{2}}{2lnx}$(x>1),得g′(x)=-$\frac{x(2lnx-1)}{{2ln}^{2}x}$,
若1<x<$\sqrt{e}$,则g′(x)>0,若x>$\sqrt{e}$,则g′(x)<0,
得g(x)在(1,$\sqrt{e}$)递增,在($\sqrt{e}$,+∞)递减,
故g(x)=-$\frac{{x}^{2}}{2lnx}$(x>1)的最大值是g($\sqrt{e}$)=-e,
故a>-e,
综上a>-e.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{{\sqrt{3}π}}{24}$ | D. | $1-\frac{{\sqrt{3}π}}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 8 | C. | 18 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | -2016 | C. | 2017 | D. | -2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “|x|<2”是“x2-x-6<0”的充分不必要条件 | |
| C. | 命题“存在∈R,使得x2+x+1<0”的否定是“对任意x∈R,均有x2+x+1≥0” | |
| D. | 若p∧q为假命题,则p,q均为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
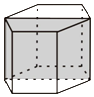 如图,已知正六棱柱的最大对角面的面积为4m2,互相平行的两个侧面的距离为 2m,则这个六棱柱的体积为( )
如图,已知正六棱柱的最大对角面的面积为4m2,互相平行的两个侧面的距离为 2m,则这个六棱柱的体积为( )| A. | 3m3 | B. | 6m3 | C. | 12m3 | D. | 15m3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com