
【题目】已知f(x)=log2(2x+a)的定义域为(0,+∞).
(1)求a的值;
(2)若g(x)=log2(2x+1),且关于x的方程f(x)=m+g(x)在[1,2]上有解,求m的取值范围.
【答案】
(1)解:由2x+a>0得2x>﹣a,即x>log2(﹣a),即函数的定义域为(log2(﹣a),+∞).
∵函数的定义域为(0,+∞),
∴log2(﹣a)=0,则﹣a=1,则a=﹣1
(2)解:当a=﹣1时,f(x)=log2(2x﹣1),
由f(x)=m+g(x)得m=f(x)﹣g(x)=log2(2x﹣1)﹣log2(2x+1)
=log2( ![]() )=log2(1﹣
)=log2(1﹣ ![]() ),
),
令h(x)=log2(1﹣ ![]() ),
),
则h(x)在[1,2]上为增函数,
当x=1时,h(x)取得最小值h(1)=log2 ![]() ,
,
当x=2时,h(x)取得最大值h(2)=log2 ![]() ,
,
则h(x)∈[log2 ![]() ,log2
,log2 ![]() ],
],
则要使方程f(x)=m+g(x)在[1,2]上有解,
则m∈[log2 ![]() ,log2
,log2 ![]() ]
]
【解析】(1)求出函数的定义域,根据条件建立方程进行求解即可,(2)利用参数分离法进行分类,然后利用复合函数的单调性之间的关系,构造函数求出函数的值域即可得到结论.
【考点精析】利用复合函数单调性的判断方法对题目进行判断即可得到答案,需要熟知复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
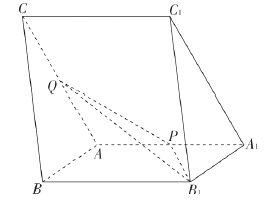
【题目】如图,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)在平面![]() 内过点
内过点![]() 作
作![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 是棱长为2的正方体
是棱长为2的正方体![]() 的棱
的棱![]() 的中点,点
的中点,点![]() 在面
在面![]() 所在的平面内,若平面
所在的平面内,若平面![]() 分别与平面
分别与平面![]() 和平面
和平面![]() 所成的锐二面角相等,则点
所成的锐二面角相等,则点![]() 到点
到点![]() 的最短距离是( )
的最短距离是( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)= ![]() 的定义域为A,m>0,函数g(x)=4 x﹣1(0<x≤m)的值域为B.
的定义域为A,m>0,函数g(x)=4 x﹣1(0<x≤m)的值域为B.
(1)当m=1时,求 (R A)∩B;
(2)是否存在实数m,使得A=B?若存在,求出m的值; 若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(ex)=ax2﹣x,a∈R.
(1)求f(x)的解析式;
(2)求x∈(0,1]时,f(x)的值域;
(3)设a>0,若h(x)=[f(x)+1﹣a]logxe对任意的x1 , x2∈[e﹣3 , e﹣1],总有|h(x1)﹣h(x2)|≤a+ ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.如图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”. 
(1)求m,n的值,并求这100名学生月消费金额的样本平均数 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8﹣200=1000(元).设购买某商品得到的实际折扣率= ![]() .设某商品标价为x元,购买该商品得到的实际折扣率为y.
.设某商品标价为x元,购买该商品得到的实际折扣率为y.
(1)写出当x∈(0,1000]时,y关于x的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(2)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于 ![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= ![]() CD=a,PD=
CD=a,PD= ![]() a.
a. 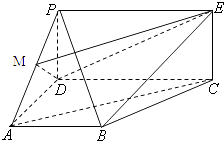
(1)若M为PA中点,求证:AC∥平面MDE;
(2)求平面PAD与PBC所成锐二面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com