
 ,求向量
,求向量 的夹角.
的夹角. |OF||y1-y2|=
|OF||y1-y2|= |y1-y2|=
|y1-y2|= ,从而有|y1-y2|=5,再设直线OA,OB的倾斜角分别为α,β,∠AOB=θ,利用斜率公式得出kOA和kOB,设θ=|α-β|,再利用夹角公式,即可求出答案.
,从而有|y1-y2|=5,再设直线OA,OB的倾斜角分别为α,β,∠AOB=θ,利用斜率公式得出kOA和kOB,设θ=|α-β|,再利用夹角公式,即可求出答案.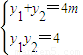 --------(2分)
--------(2分)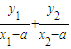 =
=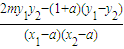
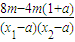 =0.∴8m-4m(1+a)=0,
=0.∴8m-4m(1+a)=0, |OF||y1-y2|=
|OF||y1-y2|= |y1-y2|=
|y1-y2|=
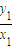 =
=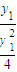 =
=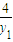 =tanα,kOB=
=tanα,kOB=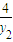 =tanβ--------(9分)
=tanβ--------(9分)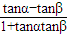 |=|
|=|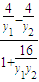 |=
|=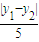 =1------(11分)
=1------(11分)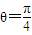 ----------------------(12分)
----------------------(12分)

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源:山东省济宁五中2010届高三5月模拟(理) 题型:填空题
已知抛物线和双曲线都经过点 ,它们在
,它们在 轴上有共同焦点,抛物线的顶点为坐
轴上有共同焦点,抛物线的顶点为坐
标原点,则双曲线的标准方程是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com