Question

（20分）在一次实战军事演习中，红方的一条直线防线上设有20个岗位。为了试验5种不同新式武器，打算安排5个岗位配备这些新式武器，要求第一个和最后一个岗位不配备新式武器，且每相邻5个岗位至少有一个岗位配备新式武器，相邻两个岗位不同时配备新式武器，问共有多少种配备新式武器的方案？

Answer 1

解析： 设20个岗位按先后排序为1，2，，… ，20，且设第k种新式武器设置的序号为 。令，，，，，

，则有

                                        （*）

其中，。       -------------------------------------- 5分

作代换 ，，从而有

                                        （**）

其中      。    ---------------------------------------------------------- 10分

现求解问题（**）:

方法一： 设I为的正整数解的全体，为I中满足的解的全体。则

上式成立的原因是，因为没有同时满足，，的的正整数组。所以

.   -------------- 15分

方法二 ：问题（**）的解数等于展开式中的系数。

而，

故只须求展开式中的系数。

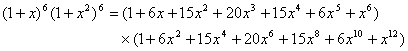
因此的系数为 6×15＋20×20＋6×15 ＝ 580。  ----------------------------------------- 15分

因为5种新式武器各不相同，互换位置得到不同的排列数，所以配备新式武器的方案数等于

。   ------------------------------------------ 20分