
| 4 |
| 5 |
| 3 |
| 4 |
| C | 1 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 8 |
| 25 |
| C | 1 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 8 |
| 3 |
| 25 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 400 |
| C | 1 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 4 |
| C | 1 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 14 |
| 400 |
| 7 |
| 200 |
| 3 |
| 25 |
| 4 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 3 |
| 4 |
| 73 |
| 400 |
| C | 1 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 3 |
| 4 |
| C | 1 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 4 |
| 5 |
| 168 |
| 400 |
| 21 |
| 50 |
| 4 |
| 5 |
| 3 |
| 4 |
| 144 |
| 400 |
| 9 |
| 25 |
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 14 |
| 400 |
| 73 |
| 400 |
| 168 |
| 400 |
| 144 |
| 400 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
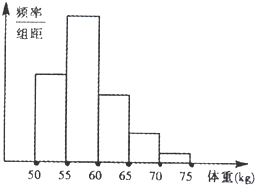 (2009•聊城一模)某校对高三年级的学生进行体检,现将高三男生的体重(单位:㎏)数据进行整理后分成五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65㎏属于偏胖,低于55㎏属于偏瘦,已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频率数为400,则该校高三年级的男生总数和体重正常的频率分别为( )
(2009•聊城一模)某校对高三年级的学生进行体检,现将高三男生的体重(单位:㎏)数据进行整理后分成五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65㎏属于偏胖,低于55㎏属于偏瘦,已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频率数为400,则该校高三年级的男生总数和体重正常的频率分别为( )查看答案和解析>>
科目:高中数学 来源: 题型:
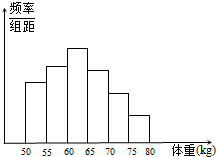 (2008•深圳二模)某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成六组,并绘制频率分布直方图(如图所示).已知图中从左到右第一、第六小组的频率分别为0.16、0.07,第一、第二、第三小组的频率成等比数列,第三、第四、第五、第六小组的频率成等差数列,且第三小组的频数为100,则该校高三年级的男生总数为( )
(2008•深圳二模)某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成六组,并绘制频率分布直方图(如图所示).已知图中从左到右第一、第六小组的频率分别为0.16、0.07,第一、第二、第三小组的频率成等比数列,第三、第四、第五、第六小组的频率成等差数列,且第三小组的频数为100,则该校高三年级的男生总数为( )查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,桂花的成活率为
,桂花的成活率为 ,假设每棵树成活与否是相互独立的.求:
,假设每棵树成活与否是相互独立的.求:查看答案和解析>>
科目:高中数学 来源:2011年安徽省安庆市高考数学二模试卷(理科)(解析版) 题型:解答题
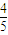 ,桂花的成活率为
,桂花的成活率为 ,假设每棵树成活与否是相互独立的.求:
,假设每棵树成活与否是相互独立的.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com