
分析 先求出函数的定义域,再求导,根据导数和函数的最值的关系求出最值即可得到函数的值域.
解答 解:y=$\frac{{x}^{2}-x+1}{{x}^{2}}$=1+$\frac{1}{{x}^{2}}$-$\frac{1}{x}$,函数的定义域为(-∞,0)∪(0,+∞)
∴y′=$\frac{1}{{x}^{2}}$-$\frac{2}{{x}^{3}}$=$\frac{x-2}{{x}^{3}}$,
当y′>0时,解得x<0或x>2,函数单调递增,
当y′<0时,解得0<x<2,函数单调递减,
当x=2时,函数有最小值,最小值为y=1+$\frac{1}{4}$-$\frac{1}{2}$=$\frac{3}{4}$,无最大值,
故值域为[$\frac{3}{4}$,+∞),
故答案为:[$\frac{3}{4}$,+∞)
点评 本题考查了函数的值域的求法,采用导数和函数的最值的关系即可求出,属于中档题.


科目:高中数学 来源: 题型:解答题
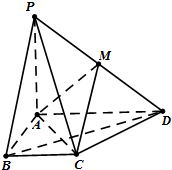 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2,M 为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2,M 为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(文)试卷(解析版) 题型:选择题
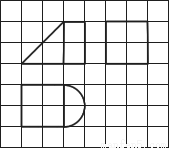
如图,网格纸上小正方形的边长为 ,粗实线画出的是某几何体的三视图,则该几何体的的体积为( )
,粗实线画出的是某几何体的三视图,则该几何体的的体积为( )
 B.
B. C.
C.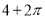 D.
D.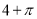
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(理)试卷(解析版) 题型:选择题
如图,网格纸上小正方形的边长为 ,粗实线画出的是某几何体的三视图,则该几何体的的体积为( )
,粗实线画出的是某几何体的三视图,则该几何体的的体积为( )

 B.
B. C.
C.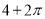 D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
在等差数列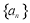 中,
中,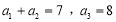 .令
.令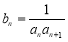 ,数列
,数列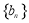 的前
的前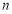 项和为
项和为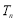 .
.
(1)求数列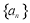 的通项公式;
的通项公式;
(2)求数列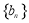 的前
的前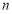 项和
项和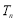 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com