练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图,已知a∥b∥c,直线d与a、b、c相交于A、B、C三点.

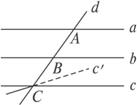
    求证:a、b、c、d四线共面.

    证法一:∵a∥b,∴由a、b可确定一个平面α,而A∈a,aα,故A∈α.同理,B∈α.

    故直线ABα,即dα.

    又b∥c,故由b、c可确定平面β,

    而B∈β,C∈β,

    ∴直线BCβ,即dβ.

    这样相交直线b、d既在α内又在β内.

    从而α与β重合,∴a、b、c、d四线共面.

    证法二:∵a∥b,∴a、b可确定平面α.

    又A∈α,B∈α,∴直线ABα,即dα.

    假设cα.∵C∈α,∴c∩α=C.

    过C点作直线c′∥a,

    又a∥c,∴c∥c′.

    这与c∩c′=C相矛盾.

    ∴直线cα.∴直线a、b、c、d四线共面.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

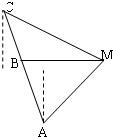    精英家教网如图，已知A、B、C是一条直路上的三点，AB与BC各等于1千米，从三点分别遥望塔M，在A处看见塔在北偏东45方向，在B处看见塔在正东方向，在C处看见塔在南偏东60°方向，求塔到直路ABC的最短距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知A、B、C、D四点共圆，延长AD和BC相交于点E，AB=AC．
    （1）证明：AB2=AD•AE；
    （2）若EG平分∠AEB，且与AB、CD分别相交于点G、F，证明：∠CFG=∠BGF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知A、B、C是长轴为4的椭圆上的三点，点A是长轴的右顶点，BC过椭圆中心O，且
    AC
    •
    BC
    =0，|
    BC
    |=2|
    AC
    |    ，
    （1）求椭圆的标准方程；
    （2）若过C关于y轴对称的点D作椭圆的切线DE，则AB与DE有什么位置关系？证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源：选修设计数学A4－1人教版 人教版 题型：022

    如图，已知a∥b∥c，直线m、n分别与直线a、b、c交于点A、B、C和点、、，如果AB＝BC＝1，＝，则＝________．

    查看答案和解析>>

    科目：高中数学 来源：2010年河南省焦作市高二下学期期末考试数学卷 题型：填空题

    如图，已知A,B,C,D,E,为圆上五个点，且CD∥AB,AD=CD=BC,∠ADC=120°.则∠AEB=           

                   .

     

    查看答案和解析>>

    同步练习册答案