Question

求下列各式中参数a的范围：

(1)＜；(2)＞．

Answer 1

答案：
解析：

　　解：(1)因为幂函数y＝的单调减区间为(－∞，0)和(0，＋∞)，故要分下列情况讨论：

　　

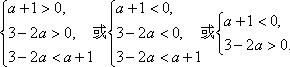
　　解上面的不等式组：得＜a＜或a＜－1．综上可得a的范围是(－∞，－1)∪(，)．

　　(2)函数y＝为偶函数，在(0，＋∞)上为单调递减，在(－∞，0)上单调递增．由＞可得0＜|a－1|＜|2＋a|，解得a＞，且a≠1．所以a的范围是(，1)∪(1，＋∞)．

　　点评：利用幂函数的单调性求参数的问题时，需注意：找准相应的幂函数，准确判断幂函数的奇偶性和单调性；定义域不要遗漏；注意分类讨论的思想．

提示：

已知同指数的两个幂值的大小，可以利用幂函数的单调性进行比较自变量即可，但是要注意幂函数的定义域、单调性和奇偶性．