
四面体的五条棱长都是2,另一条棱长为1,则四面体的体积为( )
A.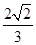 B.
B.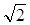 C.
C.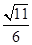 D.
D.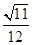
C
【解析】
试题分析:根据已知题意可知
四面体的五条棱长都是2,另一条棱长为1,那么说明了设以1为棱长所在的平面ABC,另外的顶点为D,则设AB=1,取AB的中点E,那么连接DE,CE,则可知AB垂直平面CDE,那么可知将所求的体积分为两个同底面的三棱锥的体积和,高为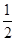 ,底面CDE的面积,利用已知的边长和等腰三角形的性质,可知其高为
,底面CDE的面积,利用已知的边长和等腰三角形的性质,可知其高为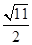 ,底边为2=CD,那么则四面体的体积为
,底边为2=CD,那么则四面体的体积为
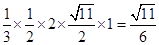 ,故选C.
,故选C.
考点:本试题考查了四面体的体积知识。
点评:解决该试题的关键是利用已知的边的长度找到一个棱的垂面,然后将所求的几何体转换为有确定形状的几何体的体积来求解,这是问题的核心,也是入手点,属于中档题。


科目:高中数学 来源:2012-2013学年安徽省高三上学期第二次模拟理科数学试卷(解析版) 题型:选择题
四面体的五条棱长都是2,另一条棱长为1,则四面体的体积为( )。
A.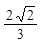 B.
B.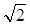 C.
C.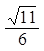 D.
D.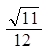
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市金乡一中高一(下)2月月考数学试卷(解析版) 题型:选择题

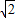
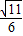
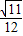
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com