Question

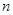（12分）连续抛两次质地均匀的骰子得到的点数分别为和，将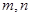作为Q点的横、纵坐标，

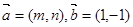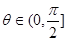（1）记向量的夹角为，求的概率；

（2）求点Q落在区域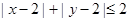内的概率．

 

Answer 1

【答案】

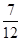（1）；（2）.

【解析】

试题分析：(1)总的基本事件的个数有(1,1),(1,2),...,(6,6)共36个结果；

那么由于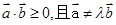,所以，所以此事件包含的基本结果共有21个,

所以此事件的概率为.

(2)作出不等式表示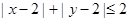表示的平面区域可知是一个正方形，此正方形内包含横纵坐标都为正整数的点有11个，所以其概率为.

考点：向量的夹角，向量的数量积，线性规划，古典概型概率.

点评：根据向量夹角的范围可知向量的数量积大于零，据此可得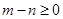,从而得到(1,1),(1,2),...(6,6)共36个点中有21个满足，然后根据古典概型概率计算公式计算即可.

第（2）问关键是正确作出不等式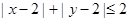表示的平面区域可知是一个正方形,然后找出此正方形包括边上的整点个数，再根据古典概型概率计算公式计算即可.