
| ��ͼ�����Ա��� | �ú�����ֵ���� | |
| �ڣ�a��b���ڣ����������x��f��x����g��x������ | �� | �� |
| �ڣ�a��b���ڣ�������x0��ʹf��x����g��x������ | �� | �� |
���� ��1����$x��[\frac{��}{6}��\frac{��}{2}]$���ɵ�$��2x+\frac{��}{3}��$��$[\frac{2��}{3}��\frac{4��}{3}]$������$sin��2x+\frac{��}{3}��$��$[-\frac{\sqrt{3}}{2}��1]$�����$\frac{1}{a}$��$-\frac{\sqrt{3}}{2}$��������ɵó���
��2������ʽx2-2ax+2a+1��0��Ϊa��2-2x��+x2+1��0�����ڶ�0��x��1������ʵ��x������������һ�κ����ĵ����Լ��ɵó���
��3������ʽ$f��x����\frac{1}{2}$����Ϊu��x��=x2-$\frac{1}{2}$��ax������ͼ���ɵó���
��4���ֱ�����f��x����g��x����ͼ���ɵó���
��� 
 �⣺��1����$x��[\frac{��}{6}��\frac{��}{2}]$����$��2x+\frac{��}{3}��$��$[\frac{2��}{3}��\frac{4��}{3}]$��
�⣺��1����$x��[\frac{��}{6}��\frac{��}{2}]$����$��2x+\frac{��}{3}��$��$[\frac{2��}{3}��\frac{4��}{3}]$��
��$sin��2x+\frac{��}{3}��$��$[-\frac{\sqrt{3}}{2}��1]$��
��$\frac{1}{a}$��$-\frac{\sqrt{3}}{2}$��
���$-\frac{2\sqrt{3}}{3}$��a��0��
��a��ȡֵ��Χ��$��-\frac{2\sqrt{3}}{3}��0��$��
��2������ʽx2-2ax+2a+1��0��Ϊa��2-2x��+x2+1��0��
�߶�0��x��1������ʵ��x��������
��$\left\{\begin{array}{l}{2a+1��0}\\{2��0}\end{array}\right.$�����$a��-\frac{1}{2}$��
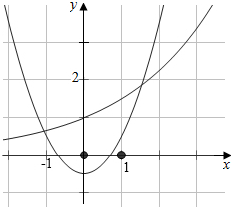
��3������ʽ$f��x����\frac{1}{2}$����Ϊu��x��=x2-$\frac{1}{2}$��ax������ͼ��1��aʱ���ɵã���-1��2-$\frac{1}{2}$��a-1�����1��a��2��ͬ���ɵã���0��a��1ʱ��${1}^{2}-\frac{1}{2}$��a1�����$\frac{1}{2}��a��1$��
���Ͽɵ�a��ȡֵ��Χ�ǣ�$��\frac{1}{2}��1��$�ȣ�1��2����
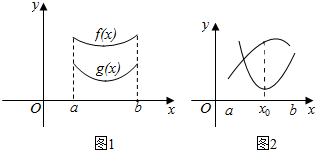
��4������ͼ��ʾ�������䣨a��b���ڣ�����y=f��x����ͼ���ں���y=g��x����ͼ����Ϸ���
�ں���[f��x��-g��x��]min��0��
����ͼ��ʾ������x0�ʣ�a��b����ʹ�ú���y=f��x����ͼ����x=x0�ĵ��ں���y=g��x����ͼ����x=x0����Ϸ���
�ܴ���x0�ʣ�a��b����f��x0��-g��x0����0��
���� ���⿼���˺�����ͼ�������ʣ����������ν��˼�뷽����������������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {��1��0��} | B�� | {��-1��1��} | C�� | {��2��0��} | D�� | {��2��1��} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��+�ޣ� | B�� | ��1��+�ޣ� | C�� | ��0��+�ޣ� | D�� | ��-�ޣ�0�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com