
分析 (1)设P(x0,y0)(x≠±a),Q(x,y).由条件$\left\{\begin{array}{l}{\frac{y}{x+a}•\frac{{y}_{0}}{{x}_{0}+a}=-1}\\{\frac{y}{x-a}•\frac{{y}_{0}}{{x}_{0}-a}=-1}\end{array}\right.$,解得x0,y0,代入双曲线化简即可得出.
(2)设Q(x,y),P(x1,y1),则$\frac{{x}_{1}^{2}}{{a}^{2}}$-$\frac{{y}_{1}^{2}}{{b}^{2}}$=1,$\frac{{x}_{0}^{2}}{{a}^{2}}-\frac{{y}_{0}^{2}}{{b}^{2}}$=1.可得$\frac{{x}_{1}^{2}-{x}_{0}^{2}}{{a}^{2}}$=$\frac{{y}_{1}^{2}-{y}_{0}^{2}}{{b}^{2}}$.根据MP⊥MQ,NP⊥NQ,可得$\overrightarrow{MP}•\overrightarrow{MQ}$=(x1-x0)(x-x0)+(y1-y0)(y-y0)=0,$\overrightarrow{NP}•\overrightarrow{NQ}$=(x1+x0)(x+x0)+(y1+y0)(y+y0)=0,于是$({x}_{1}^{2}-{x}_{0}^{2})$$({x}^{2}-{x}_{0}^{2})$+$({y}_{1}^{2}-{y}_{0}^{2})$$({y}^{2}-{y}_{0}^{2})$=0,即可得出根据方程.
解答 解:(1)设P(x0,y0)(x≠±a),Q(x,y).
∵A1(-a,0),A2(a,0).
由条件$\left\{\begin{array}{l}{\frac{y}{x+a}•\frac{{y}_{0}}{{x}_{0}+a}=-1}\\{\frac{y}{x-a}•\frac{{y}_{0}}{{x}_{0}-a}=-1}\end{array}\right.$,则$\left\{\begin{array}{l}{{x}_{0}=-x(x≠±a)}\\{{y}_{0}=\frac{{x}^{2}-{a}^{2}}{y}}\end{array}\right.$,
而点P(x0,y0)在双曲线上,∴b2x02-a2y02=a2b2.
即b2(-x2)-a2($\frac{{x}^{2}-{a}^{2}}{y}$)2=a2b2
化简得Q点的轨迹方程为:a2x2-b2y2=a4(x≠±a).
(2)设Q(x,y),P(x1,y1),则$\frac{{x}_{1}^{2}}{{a}^{2}}$-$\frac{{y}_{1}^{2}}{{b}^{2}}$=1,$\frac{{x}_{0}^{2}}{{a}^{2}}-\frac{{y}_{0}^{2}}{{b}^{2}}$=1.
∴$\frac{{x}_{1}^{2}-{x}_{0}^{2}}{{a}^{2}}$=$\frac{{y}_{1}^{2}-{y}_{0}^{2}}{{b}^{2}}$(*)
∵MP⊥MQ,NP⊥NQ,
∴$\overrightarrow{MP}•\overrightarrow{MQ}$=(x1-x0)(x-x0)+(y1-y0)(y-y0)=0,
$\overrightarrow{NP}•\overrightarrow{NQ}$=(x1+x0)(x+x0)+(y1+y0)(y+y0)=0,
∴$({x}_{1}^{2}-{x}_{0}^{2})$$({x}^{2}-{x}_{0}^{2})$+$({y}_{1}^{2}-{y}_{0}^{2})$$({y}^{2}-{y}_{0}^{2})$=0,(**)
把(*)代入(**)可得:a2x2-b2y2=${a}^{2}{x}_{0}^{2}$-${b}^{2}{y}_{0}^{2}$.
点评 本题考查了求轨迹方程的方法、数量积于是性质、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 视力 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 1.0 | 1.2 | 1.5 |
| 人数 | 1 | 1 | 3 | 4 | 3 | 4 | 4 | 6 | 8 | 10 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“如果p2+q2=2,则p+q≤2”的否命题是“如果p+q>2,则p2+q2≠2” | |
| B. | 命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∨q为假 | |
| C. | “若am2<bm2,则a<b”的逆命题为真命题 | |
| D. | 若${(\sqrt{x}-\frac{1}{{2\root{3}{x}}})^n}$的展开式中第四项为常数项,则n=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
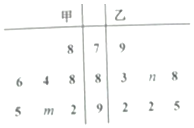 甲、乙两名同学在高一上学期7次物理考试成绩的茎叶图如图所示,其中甲成绩的平均数是88,乙学生的成绩中位数是89,则n-m的值是( )
甲、乙两名同学在高一上学期7次物理考试成绩的茎叶图如图所示,其中甲成绩的平均数是88,乙学生的成绩中位数是89,则n-m的值是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com