【答案】
分析:法一:
(Ⅰ)由S
n2=a
13+a
23+…+a
n3,知S
n-12=a
13+a
23+…+a
n-13,两式相减,得
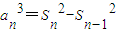
=a
n(S
n+S
n-1),由a
n>0,知
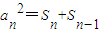
(n≥2),故
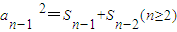
,两式相减,得
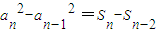
=a
n+a
n-1,由此能够证明数列{a
n}为等差数列,通项公式为a
n=n.
(Ⅱ)
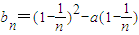
=
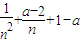
,令
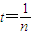
,则
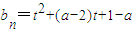
,设g(t)=t
2+(a-2)t+1-a,当a<

时,g(t)在(0,

]上为减函数,由此能求出实数a的取值范围.
法二:
(Ⅰ)同法一.
(Ⅱ)
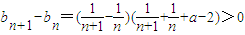
,故
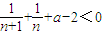
,由此能求出实数a的取值范围.
解答:解:法一:
(Ⅰ)∵S
n2=a
13+a
23+…+a
n3,
∴S
n-12=a
13+a
23+…+a
n-13,
两式相减,得
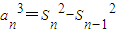
=(S
n-S
n-1)(S
n+S
n-1)=a
n(S
n+S
n-1),
∵a
n>0,∴
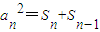
(n≥2),
∴
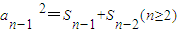
,
两式相减,得
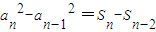
=a
n+a
n-1,
∴a
n-a
n-1=1(n>3),
∵
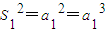
,且a
1>0,∴a
1=1,
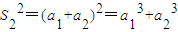
,
∴(1+a
2)
2=1+
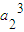
,∴
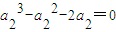
,
由a
2>0,得a
2=2,
∴a
n-a
n-1=1,n≥2,
故数列{a
n}为等差数列,通项公式为a
n=n.
(Ⅱ)
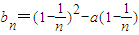
=
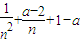
,
令
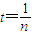
,则
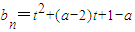
,
设g(t)=t
2+(a-2)t+1-a,
当
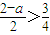
时,即a<

时,g(t)在(0,

]上为减函数,
且
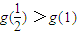
,∴b
1<b
2<b
3<…
当
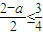
时,即
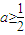
时,
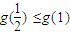
,从而b
2≤b
1不合题意,
∴实数a的取值范围
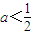
.
法二:
(Ⅰ)同法一.
(Ⅱ)
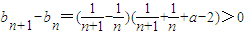
,
∴
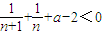
,
即
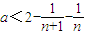
对任意n∈N
*成立,
∴实数a的取值范围
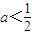
.
点评:本题考查等差数列的证明和通项公式的求法,考查实数取值范围的求法.考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

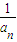 )2-a(1-
)2-a(1- ),若bn+1>bn对任意n∈N*恒成立,求实数a的取值范围.
),若bn+1>bn对任意n∈N*恒成立,求实数a的取值范围.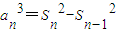 =an(Sn+Sn-1),由an>0,知
=an(Sn+Sn-1),由an>0,知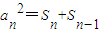 (n≥2),故
(n≥2),故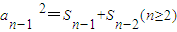 ,两式相减,得
,两式相减,得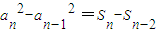 =an+an-1,由此能够证明数列{an}为等差数列,通项公式为an=n.
=an+an-1,由此能够证明数列{an}为等差数列,通项公式为an=n.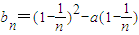 =
=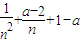 ,令
,令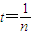 ,则
,则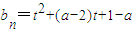 ,设g(t)=t2+(a-2)t+1-a,当a<
,设g(t)=t2+(a-2)t+1-a,当a< 时,g(t)在(0,
时,g(t)在(0, ]上为减函数,由此能求出实数a的取值范围.
]上为减函数,由此能求出实数a的取值范围.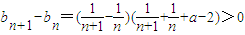 ,故
,故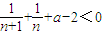 ,由此能求出实数a的取值范围.
,由此能求出实数a的取值范围.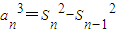 =(Sn-Sn-1)(Sn+Sn-1)=an(Sn+Sn-1),
=(Sn-Sn-1)(Sn+Sn-1)=an(Sn+Sn-1),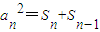 (n≥2),
(n≥2),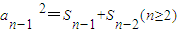 ,
,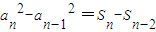 =an+an-1,
=an+an-1,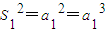 ,且a1>0,∴a1=1,
,且a1>0,∴a1=1,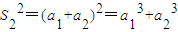 ,
,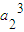 ,∴
,∴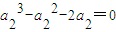 ,
,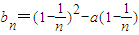 =
=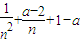 ,
,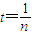 ,则
,则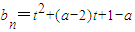 ,
,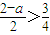 时,即a<
时,即a< 时,g(t)在(0,
时,g(t)在(0, ]上为减函数,
]上为减函数,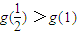 ,∴b1<b2<b3<…
,∴b1<b2<b3<…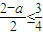 时,即
时,即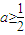 时,
时,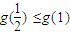 ,从而b2≤b1不合题意,
,从而b2≤b1不合题意,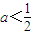 .
.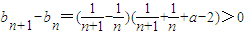 ,
,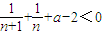 ,
,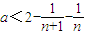 对任意n∈N*成立,
对任意n∈N*成立,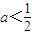 .
.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案