
| 1 |
| 2 |
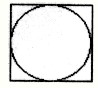 解:(1)正方形内切圆半径
解:(1)正方形内切圆半径| 1 |
| 2 |
| π |
| 4 |
| S圆 |
| S正方形 |
| ||
| 1 |
| π |
| 4 |
. |
| A |
. |
| A |
| 3 |
| 21 |
| 3 |
| 21 |
| 18 |
| 21 |
| 6 |
| 7 |


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源:2014届山西省高一下学期期中理科数学试卷(解析版) 题型:解答题
口袋中有大小、形状都相同的6个球,其中白球2个,红球4个,
(1)任取一个球投在一个面积为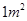 的正方形内,求球落在正方形内切圆内的概率;
的正方形内,求球落在正方形内切圆内的概率;
(2)若在袋中一次任取两个,求取到红球的概率.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省南京师大附属实验学校高二(下)期中数学试卷(文科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2008-2009学年山东省聊城市高唐一中(下)模块数学试卷(必修3)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com