
已知a>0,函数f(x)=ax-bx2.
(1)当b>0时,若对任意x∈R都有f(x)≤1,证明a≤2![]() ;
;
(2)当b>1时,证明:对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2![]() ;
;
(3)当0<b≤1时,讨论:对任意x∈[0,1],|f(x)|≤1的充要条件.
(1)证明:根据题设,对任意x∈R,都有f(x)≤1.又f(x)=-b(x- (2)证明:必要性:对任意x∈[0,1],|f(x)|≤1 f(1)≥-1,即a-b≥-1,∴a≥b-1. 对任意x∈[0,1],|f(x)|≤1 充分性:因为b>1,a≥b-1,对任意x∈[0,1],可以推出ax-bx2≥b(x-x2)-x≥-x≥-1,即ax-bx2≥-1,因为b>1,a≤2 ax-bx2≤2 综上,当b>1时,对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2 (3)解:因为a>0,0<b≤1时,对任意x∈[0,1]有f(x)=ax-bx2≥-b≥-1,即f(x)≥-1; f(x)≤1 所以,当a>0,0<b≤1时,对任意x∈[0,1],|f(x)|≤1的充要条件是a≤b+1.
|


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源:2012-2013学年河北省石家庄市高三下学期第二次质量检测理科数学试卷(解析版) 题型:解答题
.(本小题满分12分)
已知函數f(x)=ln+mx2(m∈R)
(I)求函数f(x)的单调区间;
(II)若m=0,A(a,f(a))、B(b,f(b))是函数f(x)图象上不同的两点,且a>b>0, 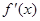 为f(x)的导函数,求证:
为f(x)的导函数,求证:
(III)求证 
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=loga(ax-1)(a>0且a≠1)
(1)求f(x)的定义域;
(2)讨论f(x)的单调性;
(3)x为何值时,函数值大于1.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=a-![]() 是偶函数,a为实常数.
是偶函数,a为实常数.
(1)求b的值;
(2)当a=1时,是否存在n>m>0,使得函数y=f(x)在区间[m,n]上的函数值组成的集合也是[m,n],若存在,求出m,n的值,否则,说明理由.
(3)若在函数定义域内总存在区间[m,n](m<n),使得y=f(x)在区间[m,n]上的函数值组成的集合也是[m,n],求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知指函数ƒ(x)=ax(a>0,且a≠1)自变量与函数值 的部分对应值如右表:
那么a=_____;若函数y=x[ƒ(x)-2],则满足条件y>0的x的集合为___________________.
| x | -1 | 0 | 2 |
| ƒ(x) | 2 | 1 | 0.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com