
已知抛物线的顶点在坐标原点,焦点为 ,点
,点 是点
是点 关于
关于 轴的对称点,过点
轴的对称点,过点 的直线交抛物线于
的直线交抛物线于 两点。
两点。
(1)试问在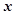 轴上是否存在不同于点
轴上是否存在不同于点 的一点
的一点 ,使得
,使得 与
与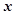 轴所在的直线所成的锐角相等,若存在,求出定点
轴所在的直线所成的锐角相等,若存在,求出定点 的坐标,若不存在说明理由。
的坐标,若不存在说明理由。
(2)若 的面积为
的面积为 ,求向量
,求向量 的夹角;
的夹角;
(1)存在T(1,0)(2)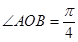
【解析】
试题分析:(1)由题意知:抛物线方程为: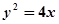 且
且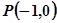 -1分
-1分
设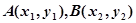
设直线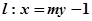 代入
代入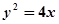 得
得
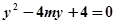
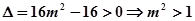
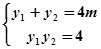 2分
2分
假设存在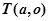 满足题意,则
满足题意,则
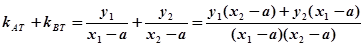
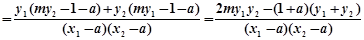
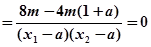
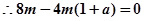 5分
5分
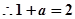
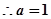
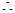 存在T(1,0)
-6分
存在T(1,0)
-6分
(2)(法一)
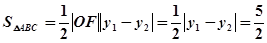
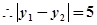 7分
7分
设直线OA,OB的倾斜角分别为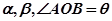
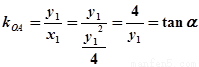 ,
,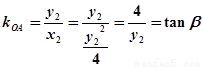 9分
9分
设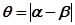
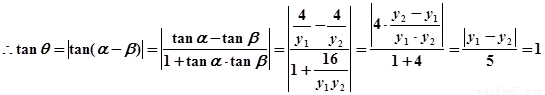 11分
11分
 12分
12分
法二: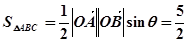
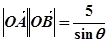 7分
7分
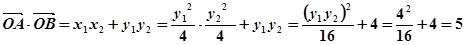 9分
9分
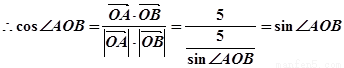
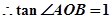 11分
11分
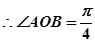 12分
12分
考点:本题考查了抛物线的方程及直线与抛物线的关系
点评:解答抛物线综合题时,应根据其几何特征熟练的转化为数量关系(如方程、函数),再结合代数方法解答,这就要学生在解决问题时要充分利用数形结合、设而不求、弦长公式及韦达定理综合思考,重视对称思想、函数与方程思想、等价转化思想的应用。


科目:高中数学 来源:山东省济宁五中2010届高三5月模拟(理) 题型:填空题
已知抛物线和双曲线都经过点 ,它们在
,它们在 轴上有共同焦点,抛物线的顶点为坐
轴上有共同焦点,抛物线的顶点为坐
标原点,则双曲线的标准方程是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com