
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 平面
平面![]() ,
,![]()
![]()
![]() 在棱
在棱![]() 上.
上.

(I)当![]() 时,求证
时,求证![]() 平面
平面![]()
(II)当二面角![]() 的大小为
的大小为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】
(Ⅰ)在平行四边形![]() 中,
中,
由![]() ,
,![]() ,
,![]() ,
,
易知![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,∴
,∴![]() ,
,
在直角三角形![]() 中,易得
中,易得![]() ,
,
在直角三角形![]() 中,
中,![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() ,
,
可得![]()
![]() .
.
∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)可知,![]() ,
,![]() ,
,
可知![]() 为二面角
为二面角![]() 的平面角,
的平面角,
![]() ,此时
,此时![]() 为
为![]() 的中点.
的中点.
过![]() 作
作![]() ,连结
,连结![]() ,则平面
,则平面![]() 平面
平面![]() ,
,
作![]() ,则
,则![]() 平面
平面![]() ,连结
,连结![]() ,
,
可得![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
因为![]() ,
,![]() ,
,
所以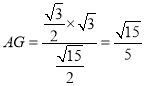 .
.
在![]() 中,
中,![]() ,
,
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
解法二:依题意易知![]() ,
,![]() 平面ACD.以A为坐标原点,AC、AD、SA分别为
平面ACD.以A为坐标原点,AC、AD、SA分别为![]() 轴建立空间直角坐标系,则易得
轴建立空间直角坐标系,则易得![]() ,
,

(Ⅰ)由![]() 有
有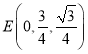 ,
,
易得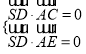 ,从而
,从而![]() 平面
平面![]() .
.
(Ⅱ)由![]() 平面
平面![]() ,二面角
,二面角![]() 的平面角
的平面角![]() .
.
又![]() ,则
,则![]() 为
为![]() 的中点,
的中点,
即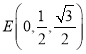 ,
,
设平面![]() 的法向量为
的法向量为![]()
则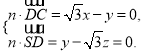 ,令
,令![]() ,得
,得![]() ,
,
从而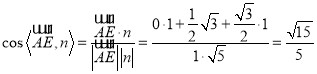 ,
,
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(Ⅰ)求证:![]() ∥平面
∥平面![]()
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角为300?如果存在,求出线段
所成的角为300?如果存在,求出线段![]() 的长;如果不存在,说明理由.
的长;如果不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经济订货批量模型,是目前大多数工厂、企业等最常采用的订货方式,即某种物资在单位时间的需求量为某常数,经过某段时间后,存储量消耗下降到零,此时开始订货并随即到货,然后开始下一个存储周期,该模型适用于整批间隔进货、不允许缺货的存储问题,具体如下:年存储成本费![]() (元)关于每次订货
(元)关于每次订货![]() (单位)的函数关系
(单位)的函数关系![]() ,其中
,其中![]() 为年需求量,
为年需求量,![]() 为每单位物资的年存储费,
为每单位物资的年存储费,![]() 为每次订货费. 某化工厂需用甲醇作为原料,年需求量为6000吨,每吨存储费为120元/年,每次订货费为2500元.
为每次订货费. 某化工厂需用甲醇作为原料,年需求量为6000吨,每吨存储费为120元/年,每次订货费为2500元.
(1)若该化工厂每次订购300吨甲醇,求年存储成本费;
(2)每次需订购多少吨甲醇,可使该化工厂年存储成本费最少?最少费用为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知表1和表2是某年部分日期的天安门广场升旗时刻表.
表1:某年部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
1月1日 | 7:36 | 4月9日 | 5:46 | 7月9日 | 4:53 | 10月8日 | 6:17 |
1月21日 | 7:31 | 4月28日 | 5:19 | 7月27日 | 5:07 | 10月26日 | 6:36 |
2月10日 | 7:14 | 5月16日 | 4:59 | 8月14日 | 5:24 | 11月13日 | 6:56 |
3月2日 | 6:47 | 6月3日 | 4:47 | 9月2日 | 5:42 | 12月1日 | 7:16 |
3月22日 | 6:15 | 6月22日 | 4:46 | 9月20日 | 5:59 | 12月20日 | 7:31 |
表2:某年2月部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
2月1日 | 7:23 | 2月11日 | 7:13 | 2月21日 | 6:59 |
2月3日 | 7:22 | 2月13日 | 7:11 | 2月23日 | 6:57 |
2月5日 | 7:20 | 2月15日 | 7:08 | 2月25日 | 6:55 |
2月7日 | 7:17 | 2月17日 | 7:05 | 2月27日 | 6:52 |
2月9日 | 7:15/p> | 2月19日 | 7:02 | 2月28日 | 6:49 |
(1)从表1的日期中随机选出一天,试估计这一天的升旗时刻早于7:00的概率;
(2)甲,乙二人各自从表2的日期中随机选择一天观看升旗,且两人的选择相互独立.记![]() 为这两人中观看升旗的时刻早于7:00的人数,求
为这两人中观看升旗的时刻早于7:00的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(3)将表1和表2中的升旗时刻化为分数后作为样本数据(如7:31化为![]() ).记表2中所有升旗时刻对应数据的方差为
).记表2中所有升旗时刻对应数据的方差为![]() ,表1和表2中所有升旗时刻对应数据的方差为
,表1和表2中所有升旗时刻对应数据的方差为![]() ,判断
,判断![]() 与
与![]() 的大小(只需写出结论)
的大小(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,长轴长是短轴长的2倍.
,长轴长是短轴长的2倍.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 两点(异于点
两点(异于点![]() ),记直线
),记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,证明:
,证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com