

(1)求异面直线PA与DE所成角的余弦值;
(2)求点D到平面PAB的距离.
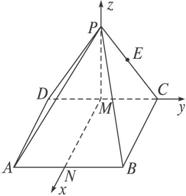
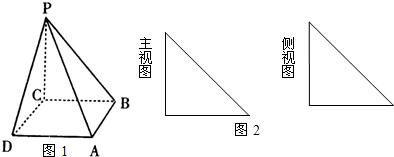
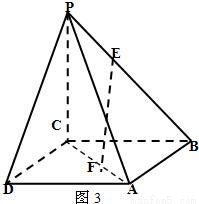
解:取DC的中点M,AB中点N,连结PM,MN,由△PDC为正三角形和PM⊥CD,又∵平面PDC⊥平面ABCD.且面PDC∩平面ABCD=CD,∴PM⊥平面ABCD,由四边形ABCD为正方形知MN⊥CD.因此以M点为原点,MN,MC,MP所在直线为x轴、y轴、z轴建立直角坐标系.

则M(0,0,0),C(0,![]() ,0),D(0,-
,0),D(0,-![]() ,0),P(0,0,
,0),P(0,0,![]() a),A(a,-
a),A(a,-![]() ,0),B(a,
,0),B(a,![]() ,0),
,0),
(1)由E为PC中点知E(0,![]() ,
,![]() a).
a).
∴![]() =(a,-
=(a,-![]() ,-
,-![]() a),
a),![]() =(0,
=(0,![]() ,
,![]() a).
a).
∴![]() ·
·![]() =-
=-![]() a2,|
a2,|![]() |=
|=![]() a,|
a,|![]() |=
|=![]() a,
a,
∴cos(![]() ,
,![]() )=
)=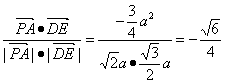 ,
,
因此异面直线PA与DE的夹角的余弦值为![]() .
.
(2)设n为平面PAB的法向量,并设n=(x,y,z),则
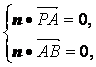
即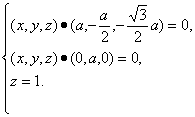
∴n=(![]() ,0,1).
,0,1).
又∵![]() =(a,0,0),
=(a,0,0),
∴d=|![]() |=
|=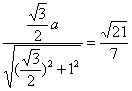 a,
a,
即点D到平面PAB的距离为![]() a.
a.


科目:高中数学 来源: 题型:
| BE |
| EP |
| CF |
| FA |
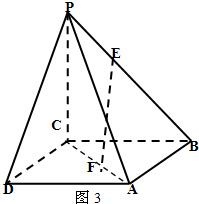
查看答案和解析>>
科目:高中数学 来源:《第二章 立体几何》2013年高考数学优化训练(解析版) 题型:解答题
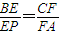 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.
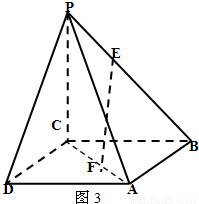
查看答案和解析>>
科目:高中数学 来源:金版人教A版数学理科:立体几何初步8(必修2、选修2-1)(解析版) 题型:解答题
 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.

查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:7 立体几何 质量检测(1)(解析版) 题型:解答题
 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.
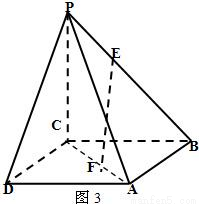
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考数学冲刺预测试卷14(文科)(解析版) 题型:解答题
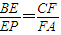 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.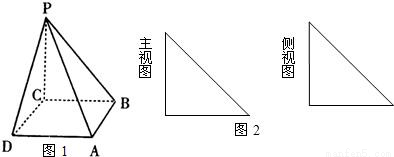
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com