
已知ABC—A1B1C1是各棱长都相等的正三棱柱,D是BC上一点,∠ADC1=90°.求二面角D—AC1—C的大小.
解:∵CC1⊥底面ABC,∠ADC1=90°, ∴由三垂线定理得BC⊥AD ∴△ABC为正三角形, ∴D为BC的中点. 过C作CE⊥C1D于E, ∵AD⊥平面BB1C1C,∴CE⊥AD, ∴CE⊥平面ADC1. 过点E作EF⊥AC1于F,连结EF,则CF⊥AC1. ∴∠EFC为二面角D—AC1—C的平面角. 设棱柱的棱长为a,则CD= 在△C1CD中,CC1=a, C1D= ∴CE= ∵△ACC1为等腰三角形, ∴CF= ∴sinCFE= ∴二面角D—AG1—C的大小为arcsin 点评:本题作二面角的平面角的方法是“垂线法”.过点D作DO⊥AC于O(易证DO⊥平面ACC1),利用DO作二面角D—AC1—C的平面角也可.
|


 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
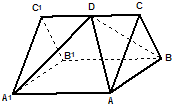 (2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点.
(2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
| ||
| 15 |
| A1P |
| A1B1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
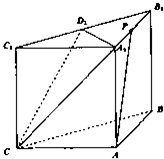 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.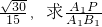 的值.
的值.查看答案和解析>>
科目:高中数学 来源:松江区二模 题型:解答题
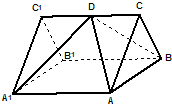
查看答案和解析>>
科目:高中数学 来源:2012年云南省昆明市高三复习适应性检测数学试卷(理科)(解析版) 题型:解答题
 的值.
的值.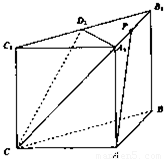
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com