
(08年安徽皖南八校联考)(本小题满分14分)
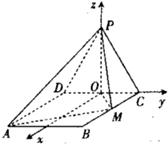
 如图所示,边长为2的等边△
如图所示,边长为2的等边△![]() 所在的平面垂直于矩形
所在的平面垂直于矩形![]() 所在的平面,
所在的平面,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() ⊥
⊥![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
解析:(法一)(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() .
.
 ∵△
∵△![]() 是等边三角形,∴
是等边三角形,∴![]() ⊥
⊥![]() ,
,
又平面![]() ⊥平面
⊥平面![]() ,
,
∴![]() ⊥平面
⊥平面![]() ,∴
,∴![]() 在平面
在平面![]() 内射影是
内射影是![]() ,
,
………………………2分
∵![]() =2,
=2,![]() ,
,![]() ,
,![]() ,
,
∴△![]() ∽△
∽△![]() ,∴
,∴![]() .
.
又![]() °,∴
°,∴![]() °,
°,
∴![]() °,∴
°,∴![]() ⊥
⊥![]() , …………………………………………………4分
, …………………………………………………4分
由三垂线定理知![]() ⊥
⊥![]() …………………………………………………………5
…………………………………………………………5
(2)解:由![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() 得
得![]() 是二面角
是二面角![]() 的平面角 …………6分
的平面角 …………6分
在Rt△![]() 中,
中,![]() ,
,![]() ,…8分
,…8分
∴![]() ,………………………………………………………………9分
,………………………………………………………………9分
![]() °,∴二面角
°,∴二面角![]() 的大小是45° ……………………………10分
的大小是45° ……………………………10分
(3)解:设![]() 到平面
到平面![]() 的距离距离是
的距离距离是![]() ,则
,则![]() , ………………11分
, ………………11分
![]() ,
,![]() ,
,
![]() .又
.又![]() ,
,![]() ,
,
 ∴
∴![]() =
=![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离距离是
的距离距离是![]() ……………………………14分
……………………………14分
(方法二)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,
,
∵△![]() 是等边三角形,∴
是等边三角形,∴![]() ⊥
⊥![]() ,
,
又∵平面![]() ⊥平面
⊥平面![]() ,
,
∴![]() ⊥平面
⊥平面![]() ,又
,又![]() 是矩形,
是矩形,
∴可建立如图所示的空间直角坐标系 …………………………………………………2分
∵![]() =2,
=2,![]() ,
,
∴![]() (
(![]() ,-1,0),
,-1,0),![]() (
(![]() ,1,0),
,1,0),![]() (0,0,
(0,0,![]() ),……………………3分
),……………………3分
∴![]() (-
(-![]() ,2,0),
,2,0),![]() (
(![]() ,1,-
,1,-![]() ),∴
),∴![]()
![]() =
=![]()
………………………………………………………………………………………4分
∴![]() ⊥
⊥![]() ,∴
,∴![]() ⊥
⊥![]() ………………………………………………………5分
………………………………………………………5分
(2)解:由(1)知平面![]() 的法向量m=
的法向量m=![]() (0,0,
(0,0,![]() )……………………6分
)……………………6分
设平面![]() 的法向量n =(
的法向量n =(![]() ,
,![]() ,
,![]() ),则n⊥
),则n⊥![]() ,n⊥
,n⊥![]() ,
,
∴![]() ,
,![]() ,
,
取![]() ,得
,得![]() ,
,![]() ………………………………………………………8分
………………………………………………………8分
n =(1,![]() ,
,![]() ),
),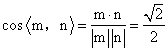 ,
,
∴二面角![]() 的大小是45° ………………………………………………10分
的大小是45° ………………………………………………10分
(3)解:![]() (0,―1,0),,
(0,―1,0),,![]() (0,-1,-
(0,-1,-![]() ) ……………………………11分
) ……………………………11分
又n =(1,![]() ,
,![]() ),∴
),∴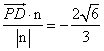 ………………………………………13分
………………………………………13分
∴点![]() 到平面
到平面![]() 的距离距离是
的距离距离是![]() . …………………………………………14分
. …………………………………………14分


科目:高中数学 来源: 题型:
(08年安徽皖南八校联考理)设![]() ,
,![]() 为两条不同直线
为两条不同直线![]() 为两个不同平面,则下列命题正确的是
为两个不同平面,则下列命题正确的是
A.![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() B.
B.![]() ∥
∥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,则
,则![]() ∥
∥![]()
C.![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() D.
D.![]() ∥
∥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,则
,则![]() ∥
∥![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年安徽皖南八校联考理)在大小相同的6个球中,有2个红球,4个黄球.若从中任意选取3个,则所选的3个球中至少有1个红球的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com