
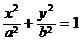 (x≥0)与半椭圆
(x≥0)与半椭圆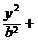
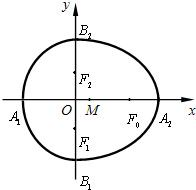
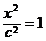 (x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0,如图,点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2分别是“果圆”与x 、y轴的交点
(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0,如图,点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2分别是“果圆”与x 、y轴的交点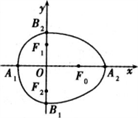
 的取值范围.
的取值范围. 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
 我们把由半椭圆
我们把由半椭圆| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |
| y2 |
| b2 |
| x2 |
| c2 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
(2007
上海,21)我们把由半椭圆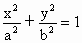 (x≥0)与半椭圆
(x≥0)与半椭圆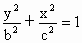 (x≤0)合成的曲线称作“果圆”,其中
(x≤0)合成的曲线称作“果圆”,其中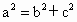 ,a>0,b>c>0.如下图,点
,a>0,b>c>0.如下图,点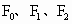 是相应椭圆的焦点,
是相应椭圆的焦点,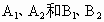 分别是“果圆”与x、y轴的交点.
分别是“果圆”与x、y轴的交点.
(1)
若△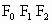 是边长为1的等边三角形,求“果圆”的方程;
是边长为1的等边三角形,求“果圆”的方程;
(2)
当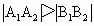 时,求
时,求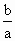 的取值范围;
的取值范围;
(3)
连接“果圆”上任意两点的线段称为“果圆”的弦.试研究:是否存在实数k,使斜率为k的“果圆”平行弦的中点轨迹总是落在某个椭圆上?若存在,求出所有可能的k值;若不存在,说明理由.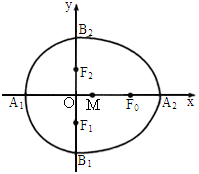
查看答案和解析>>
科目:高中数学 来源:2009届宁夏省期末数学模拟试题分类汇编(圆锥曲线) 题型:013
我们把由半椭圆![]() (x≥0)与半椭圆
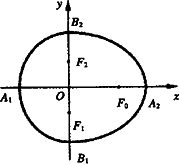
(x≥0)与半椭圆![]() 合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角,则a,b的值分别为
合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角,则a,b的值分别为
A.![]()
B.![]()
C.5,3
D.5,4
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试、文科数学(上海卷) 题型:044
我们把由半椭圆![]() (x≥0)与半椭圆
(x≥0)与半椭圆![]() (x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.
(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.
如图,设点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.

(1)若△F0F1F2是边长为1的等边三角形,求该“果圆”的方程;
(2)设P是“果圆”的半椭圆![]() (x≤0)上任意一点.求证:当|PM|取得最小值时,P在点B1,B2或A1处;
(x≤0)上任意一点.求证:当|PM|取得最小值时,P在点B1,B2或A1处;
(3)若P是“果圆”上任意一点,求|PM|取得最小值时点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com