
由(x+a)2=x2+ax+ax+a2,可知x2出现的频率为![]() ,x出现的频率为
,x出现的频率为![]() ,由此类推,(x+a)6展开后,x3出现的频率为
,由此类推,(x+a)6展开后,x3出现的频率为
![]()
![]()
![]()
![]()
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源:江苏省阜宁县中学2011-2012学年高二下学期期中调研考试数学试题 题型:022
下面使用类比推理正确的序号是________.
(1)由“(a+b)c=ac+bc”类比得到“(![]() ·
·![]() )
)![]() =
=![]()
![]() ·
·![]()
![]() ”
”
(2)由“在f(x)=ax2+bx(a≠0)中,若f(x1)=f(x2),则有f(x1+x2)=0类比得到”在等差数列{an}中,Sn为前n项的和,若Sp=Sq,则有Sp+q=0
(3)由“平面上的平行四边形的对边相等”类比得到“空间中的平行六面体的对面是全等的平行四边形”
(4)由“过圆x2+y2=r2上的点(x0,y0)的切线方程为x0x+y0y=r2”类比得到“过圆(x-a)2+(y-b)2=r2上的点(x0,y0)的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2”
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;
(Ⅰ)将两圆方程相减可得一直线方程l:x+y-4=0,该直线叫做这两圆的“根轴”,试证点P落在根轴上;
(Ⅱ)求切线长|PA|的最小值;
 (Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
(Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆O:x2+y2=1,圆C:(x-2)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|.
(1)求实数a、b间满足的![]() 等量关系;
等量关系;
(2)求切线长|PA|的最小值;
(3)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届山西省晋商四校高二下学期联考理科数学试卷(解析版) 题型:解答题
已知椭圆的长轴长为 ,焦点是
,焦点是 ,点
,点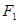 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
.
(1)求椭圆的标准方程; (2)求直线l的方程.
【解析】(1)中利用点F1到直线x=- 的距离为
的距离为 可知-
可知- +
+ =
= .得到a2=4而c=
.得到a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
得到椭圆的方程。(2)中,利用 ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。
解:(1)∵F1到直线x=- 的距离为
的距离为 ,∴-
,∴- +
+ =
= .
.
∴a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,∴所求椭圆的方程为 +y2=1.……4分
+y2=1.……4分
(2)设A(x1,y1)、B(x2,y2).由第(1)问知
 ,
,
∴ ……6分
……6分
∵A、B在椭圆 +y2=1上,
+y2=1上,
∴ ……10分
……10分
∴l的斜率为 =
= .
.
∴l的方程为y= (x-
(x- ),即
),即 x-y-
x-y- =0.
=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com