
如图,椭圆的右焦点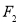 与抛物线
与抛物线 的焦点重合,过
的焦点重合,过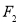 且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且
且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且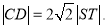
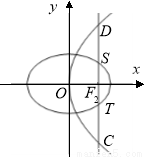
(1)求椭圆的标准方程;
(2)设P为椭圆上一点,若过点M(2,0)的直线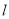 与椭圆相交于不同两点A和B,且满足
与椭圆相交于不同两点A和B,且满足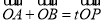 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围.
(1)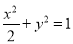 (2)
(2)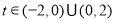
【解析】
试题分析:
(1)抛物线的方程已知,则可以求出右焦点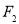 的坐标为
的坐标为 ,则可以知道
,则可以知道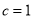 和直线CD的方程我饿哦x=1,联立直线
和直线CD的方程我饿哦x=1,联立直线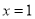 与抛物线方程可以求出C,D两点的坐标,进而得到CD的长度,再联立直线
与抛物线方程可以求出C,D两点的坐标,进而得到CD的长度,再联立直线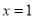 与椭圆方程即可求出ST两点的坐标,进而得到ST的距离,利用条件
与椭圆方程即可求出ST两点的坐标,进而得到ST的距离,利用条件 建立关于
建立关于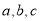 的等式,与
的等式,与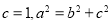 联立即可求出
联立即可求出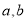 的值,进而得到椭圆的方程.
的值,进而得到椭圆的方程.
(2)因为直线l与椭圆有交点,所以直线l的斜率一定存在,则设出直线l的斜率得到直线l的方程,联立直线l与椭圆方程得到AB两点横纵坐标之间的韦达定理,即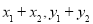 的值,再利用
的值,再利用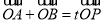 发解即可得到P点的坐标,因为P在椭圆上,代入椭圆得到直线斜率k与t的方程,
发解即可得到P点的坐标,因为P在椭圆上,代入椭圆得到直线斜率k与t的方程,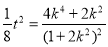 ,利用k的范围求解出函数
,利用k的范围求解出函数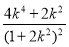 的范围即可得到t的范围.
的范围即可得到t的范围.
试题解析:
(1)设椭圆标准方程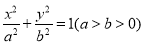 ,由题意,抛物线
,由题意,抛物线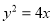 的焦点为
的焦点为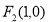 ,
,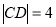 .
.
因为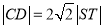 ,所以
,所以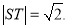 2分
2分
又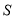
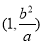 ,
,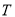
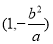 ,
,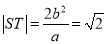 ,又
,又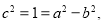
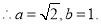
所以椭圆的标准方程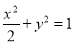 . 5分
. 5分
(2)由题意,直线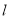 的斜率存在,设直线
的斜率存在,设直线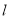 的方程为
的方程为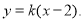
由 消去
消去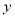 ,得
,得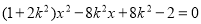 ,(*)
,(*)
设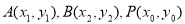 ,则
,则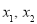 是方程(*)的两根,所以
是方程(*)的两根,所以
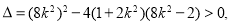 即
即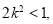 ① 7分
① 7分
且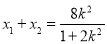 ,由
,由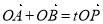 ,得
,得
若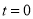 ,则
,则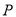 点与原点重合,与题意不符,故
点与原点重合,与题意不符,故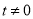 ,
,
所以,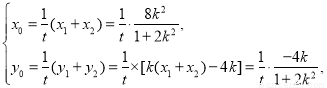 9分
9分
因为点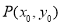 在椭圆上,所以
在椭圆上,所以
 ,即
,即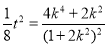
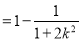 ,
,
再由①,得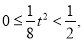 又
又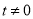 ,
,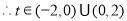 . 13分
. 13分
考点:抛物线椭圆直线与椭圆的位置关系韦达定理


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试文科数学试卷(解析版) 题型:选择题
已知直线m,n不重合,平面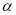 ,
,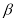 不重合,下列命题正确的是( )
不重合,下列命题正确的是( )
(A)若m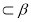 ,n
,n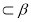 ,m//
,m//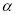 ,n//
,n//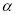 ,则
,则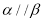
(B)若m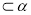 ,m
,m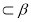 ,
,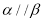 ,则m//n
,则m//n
(C)若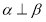 ,m
,m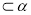 ,n
,n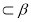 ,则
,则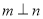
(D)若m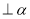 ,n
,n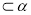 ,则
,则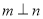
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三5月统一质量检测考试文科数学试卷(解析版) 题型:选择题
角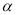 顶点在坐标原点O,始边
顶点在坐标原点O,始边 轴的非负半轴重合,点P在
轴的非负半轴重合,点P在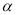 的终边上,点
的终边上,点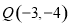 ,且
,且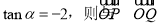 夹角的余弦值为( )
夹角的余弦值为( )
A.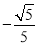 B.
B.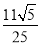 C.
C.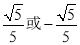 D.
D.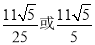
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三3月第一次模拟考试文科数学试卷(解析版) 题型:填空题
已知双曲正弦函数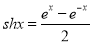 和双曲作弦函数
和双曲作弦函数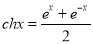 与我们学过的正弦函数和余弦函数有许多类似的性质,请类比正弦函数和余弦函数的和角公式,写出双曲正弦或双曲余弦函数的一个类似的正确结论______________.
与我们学过的正弦函数和余弦函数有许多类似的性质,请类比正弦函数和余弦函数的和角公式,写出双曲正弦或双曲余弦函数的一个类似的正确结论______________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三3月第一次模拟考试文科数学试卷(解析版) 题型:选择题
已知函数① ②
②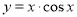 ,③
,③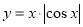 ,④
,④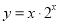 的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
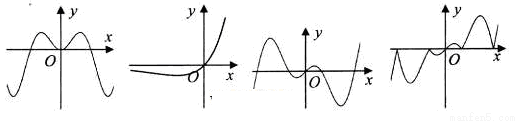
A.①④②③ B.①④③② C.④①②③ D.③④②①
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省德州市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
已知el、e2是两个单位向量,若向量a=el-2e2,b=3el+4e2,且a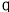 b=-6,则向量el与e2的夹角是
b=-6,则向量el与e2的夹角是
A.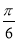 B.
B.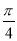 C.
C.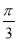 D.
D.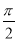
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com