Question

8．已知四面体ABCD的四个顶点都在球O的表面上，AB⊥平面BCD，又AB=3，BC=2，BD=4，且∠CBD=60°，则球O的表面积为（　　）

• A． 12π
• B． 16π
• C． 20π
• D． 25π

Answer 1

分析 由余弦定理求出CD=2$\sqrt{3}$，以AB、BC、CD、AB为长方体的长、宽、高构造长方体AGHF-BCDF，球O的半径R=$\frac{1}{2}EC$，由此能求出球O的表面积．

解答 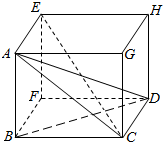解：∵四面体ABCD的四个顶点都在球O的表面上，AB⊥平面BCD，
又AB=3，BC=2，BD=4，且∠CBD=60°，
∴CD=$\sqrt{16+4-2×4×2×cos60°}$=2$\sqrt{3}$，
∴BC²+CD²=BD²，∴AB⊥平面BCD，BC⊥CD，
∴以AB、BC、CD、AB为长方体的长、宽、高构造长方体AGHF-BCDF，
则球O的半径R=$\frac{1}{2}EC$=$\frac{1}{2}\sqrt{9+4+12}$=$\frac{5}{2}$，
∴球O的表面积S=4$π×（\frac{5}{2}）^{2}$=25π．
故选：D．

点评 本题考查球的表面积的求法，是中档题，解题时要认真审题，注意构造法的合理运用．