

图1-7
思路分析:图中有直角三角形,应充分利用直角三角形的知识,设AB=5k,BC=6k(k>0),则EC=![]() BC=k,FC=
BC=k,FC=![]() CD=
CD=![]() AB=3k,得DF=2k,由勾股定理可得AE2=AB2+BE2=50k2,EF2=EC2+FC2=10k2,AF2=AD2+DF2=40k2,所以AE2=EF2+AF2.由勾股定理逆定理得Rt△AFE,又因为FG⊥AE,具备双垂直的条件,问题的解决就有了眉目.
AB=3k,得DF=2k,由勾股定理可得AE2=AB2+BE2=50k2,EF2=EC2+FC2=10k2,AF2=AD2+DF2=40k2,所以AE2=EF2+AF2.由勾股定理逆定理得Rt△AFE,又因为FG⊥AE,具备双垂直的条件,问题的解决就有了眉目.
证明:∵AB∶BC=5∶6,∴设AB=5k,BC=6k(k>0).
∴在矩形ABCD中,有CD=AB=5k,BC=AD=6k,∠B=∠C=∠D=90°.
∵EC=![]() BC,∴EC=
BC,∴EC=![]() ×6k=k.∴BE=5k.
×6k=k.∴BE=5k.
∵FC=![]() CD,∴FC=
CD,∴FC=![]() ×5k=3k.∴DF=CD-FC=2k.
×5k=3k.∴DF=CD-FC=2k.
在Rt△ADF中,由勾股定理得AF2=AD2+DF2=36k2+4k2=40k2.
同理,可得AE2=50k2,EF2=10k2.
∴AF2+EF2=40k2+10k2=50k2=AE2.∴△AEF是直角三角形.
∵FG⊥AE,∴△AFE∽△FGE.
∴EF2=GE·AE.
∵AE=![]() ,
,
∴GE=![]()
∴4GE=![]() k.
k.
∴AG=AE-GE=![]() k-
k-![]() k=
k=![]() k.∴AG=4GE.
k.∴AG=4GE.


科目:高中数学 来源: 题型:
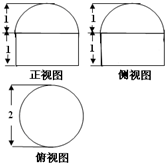
| A、4π | B、7π | C、6π | D、5π |
查看答案和解析>>
科目:高中数学 来源: 题型:
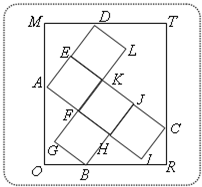 如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.
如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.| BD |
| AE |
| AF |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期模拟预测文科数学试卷(解析版) 题型:选择题
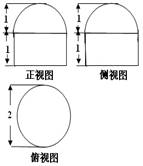
已知一个空间几何体的三视图如图1所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸,可得这个几何体的表面积是( )
A.4 B.7
B.7
C.6 D.5
D.5
查看答案和解析>>
科目:高中数学 来源:2010-2011学年宁夏高三第一次模拟考试数学文卷 题型:选择题
已知一个空间几何体的三视图如图1所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸,可得这个几何体的表面积是
(A)4 (B)7
(B)7 (C)6
(C)6 (D)5
(D)5

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com