
设函数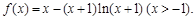
(Ⅰ)求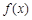 的单调区间;
的单调区间;
(Ⅱ)证明:当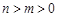 时,
时,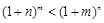 ;
;
(Ⅲ)证明:当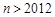 ,且
,且 …,
…, ,
,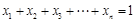 时,
时,
(1)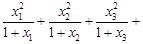 …
…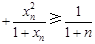
(2) 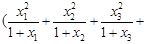 …
…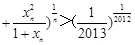 .
.
(Ⅰ)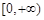 (Ⅱ)见解析(Ⅲ)见解析
(Ⅱ)见解析(Ⅲ)见解析
【解析】本试题主要是考查了导数在研究函数中的运用。求解函数的单调区间和证明不等是的综合运用。
(1)先求解函数的定义域和函数的导数,然后结合导数的符号判定单调区间。
(2)运用第一问中的结论。得到不等式的放缩得到证明。
(3)结合第一问和第二问的基础上,进一步放缩法得到结论。
解:(Ⅰ)由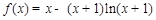 ,有
,有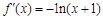 ,………………… 2分
,………………… 2分
当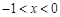 时,
时,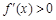 时,
时, 单调递增;
单调递增;
当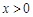 时,
时,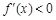 时,
时, 单调递减;
单调递减;
所以 的单调递增区间为
的单调递增区间为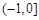 ,单调递减区间为
,单调递减区间为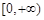 . …… 4分
. …… 4分
(Ⅱ)设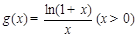 ,
,
则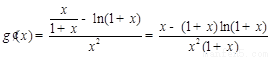 .………………6分
.………………6分
由(Ⅰ)知,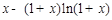 在
在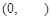 单调递减,
单调递减,
∴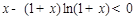 ,即
,即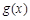 是减函数,
是减函数,
而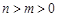 ,所以
,所以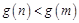 ,得
,得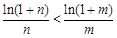 ,
,
得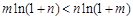 ,故
,故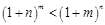 .………………… 8分
.………………… 8分
(Ⅲ)(1)由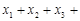 …
…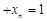 ,及柯西不等式可知,
,及柯西不等式可知,
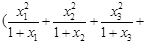 …
…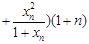
 …
…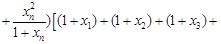 …
…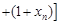
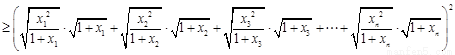
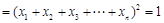 ,
,
所以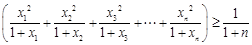 ,……………………11分
,……………………11分
(2)由(1)得: .
.
又 ,由(Ⅱ)可知
,由(Ⅱ)可知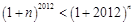 ,
,
即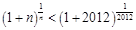 ,即
,即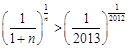 .
.
则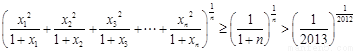 .
.
故 ………………14分
………………14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
设函数![]()
(1)求![]() 的单调增区间和单调减区间;
的单调增区间和单调减区间;
(2)若当![]() 时(其中e=2.71828…),不等式
时(其中e=2.71828…),不等式![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)若关于x的方程![]() 上恰有两个相异的实根,求实数a的取值范围。
上恰有两个相异的实根,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高三年级第一次质量检测理科数学试卷(解析版) 题型:解答题
设函数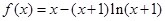 (
(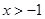 ).
).
(Ⅰ)求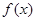 的单调区间;
的单调区间;
(Ⅱ)试通过研究函数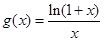 (
(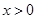 )的单调性证明:当
)的单调性证明:当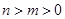 时,
时, ;
;
(Ⅲ)证明:当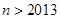 ,且
,且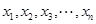 均为正实数,
均为正实数, 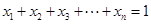 时,
时,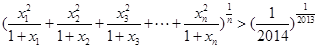 .
.
查看答案和解析>>
科目:高中数学 来源:2012届度河北省唐山市高三年级第一次模拟考试数学试卷 题型:解答题
设函数 .
.
(I )讨论f(x)的单调性;
(II) ( i )若证明:当x>6 时,
(ii)若方程f(x)=a有3个不同的实数解,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com