
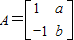 ,A的一个特征值λ=2,其对应的特征向量是
,A的一个特征值λ=2,其对应的特征向量是 .
.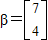 ,计算A5β的值.
,计算A5β的值. =λ
=λ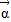 (
(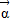 为特征向量,λ为特征值),利用矩阵的乘法法则化简求出a与b的值,代入矩阵A即可;
为特征向量,λ为特征值),利用矩阵的乘法法则化简求出a与b的值,代入矩阵A即可; =3
=3 ①,然后根据特征向量线性表示出向量β,利用矩阵的乘法法则求出β=3α1+α2②,将①和②代入A5β中求出值即可.
①,然后根据特征向量线性表示出向量β,利用矩阵的乘法法则求出β=3α1+α2②,将①和②代入A5β中求出值即可.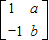
 =2
=2 ,即2+a=4,-2+b=2,解得a=2,b=4,
,即2+a=4,-2+b=2,解得a=2,b=4,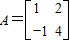 ;
;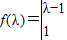
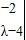 =λ2-5λ+6=0,
=λ2-5λ+6=0,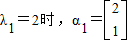 ,当λ2=3时,得
,当λ2=3时,得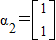 . 则A=2
. 则A=2 =3
=3
 +n
+n =
= 得:
得: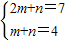 解得
解得 ,则β=3α1+α2
,则β=3α1+α2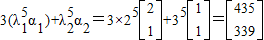 .
.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:福建省南安一中2010-2011学年高二下学期期末考试数学理科试题 题型:044
选修4-2:矩阵与变换
已知矩阵![]() ,A的一个特征值λ=2,属于λ的特征向量是
,A的一个特征值λ=2,属于λ的特征向量是![]() ,求矩阵A与其逆矩阵.
,求矩阵A与其逆矩阵.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省福州市泉港二中高三(上)第11周周考数学试卷(理科)(解析版) 题型:解答题
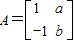 ,A的一个特征值λ=2,其对应的特征向量是
,A的一个特征值λ=2,其对应的特征向量是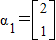 .
.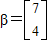 ,计算A2β的值.
,计算A2β的值.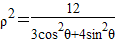 ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为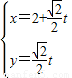 (t为参数,t∈R).求点F1,F2到直线l的距离之和.
(t为参数,t∈R).求点F1,F2到直线l的距离之和.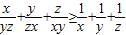 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省扬州市江都市大桥中学高一(下)期中数学试卷(解析版) 题型:解答题
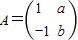 ,A的一个特征值λ=2,属于λ的特征向量是
,A的一个特征值λ=2,属于λ的特征向量是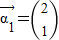 ,求矩阵A与其逆矩阵.
,求矩阵A与其逆矩阵.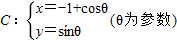 上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.
上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.查看答案和解析>>
科目:高中数学 来源:2010年江苏省镇江市丹阳市高考数学模拟试卷(解析版) 题型:解答题
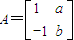 ,A的一个特征值λ=2,其对应的特征向量是
,A的一个特征值λ=2,其对应的特征向量是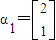 .
. ,计算A5β的值.
,计算A5β的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com