
已知函数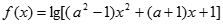 ,设命题
,设命题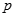 :“
:“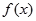 的定义域为
的定义域为 ”;
”;
命题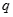 :“
:“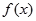 的值域为
的值域为 ” .
” .
(1)分别求命题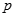 、
、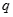 为真时实数
为真时实数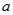 的取值范围;
的取值范围;
(2)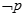 是
是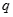 的什么条件?请说明理由.
的什么条件?请说明理由.
解析试题分析:(1)命题p可转化为恒成立问题,根据类二次函数的性质,可得到a的取值范围;命题q可转化为真数部分的值域包含(0,+∞),据些构造关于a的不等式组,解可得a的取值范围;(2)由(1)求出¬p,并比较两个命题对应的参数a的范围之间的包含关系,进而根据“谁小谁充分,谁大谁必要”可得答案.
试题解析:解:(1)命题 为真,即
为真,即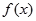 的定义域是
的定义域是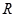 ,等价于
,等价于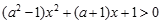 恒成立,
恒成立,
等价于 或
或
解得 或
或 .∴实数
.∴实数 的取值范围为
的取值范围为 ,
, ,
,
命题 为真,即
为真,即 的值域是
的值域是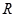 , 等价于
, 等价于 的值域
的值域 ,
,
等价于 或
或
解得 .∴实数
.∴实数 的取值范围为
的取值范围为 ,
,
(2)由(1)(2)知, :
: ;
; :
: .
.
而 ,∴
,∴ 是
是 的必要而不充分的条件
的必要而不充分的条件
考点:1.必要条件、充分条件与充要条件的判断;2.命题的真假判断与应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知向量 ,函数
,函数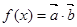
(1)求函数 的单调递减区间.
的单调递减区间.
(2)将函数 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数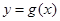 的图象.求
的图象.求 在
在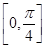
 上的值域.
上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com