
已知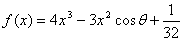 ,其中x∈R,
,其中x∈R,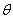 为参数,且0≤
为参数,且0≤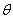 ≤
≤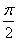 。
。
(1)当cos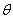 =0时,判断函数
=0时,判断函数 是否有极值;
是否有极值;
(2)要使函数 的极小值大于零,求参数
的极小值大于零,求参数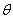 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数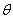 ,函数
,函数 在区间(2a – 1, a)内都是增函数,求实数a的取值范围。
在区间(2a – 1, a)内都是增函数,求实数a的取值范围。
解:(1)当cos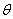 =0时,
=0时,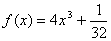 ,所以
,所以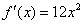 ≥0,
≥0,
则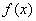 在
在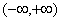 内是增函数,故无极值。
内是增函数,故无极值。
(2)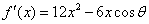 ,令
,令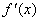 =0,得x1=0或
=0,得x1=0或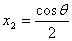 ,
由0≤
,
由0≤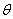 ≤
≤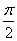 及(1)知,只需考虑cos
及(1)知,只需考虑cos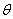 >0的情况,
>0的情况,
当x变化时,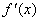 、
、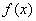 的变化情况如下表:
的变化情况如下表:
|
x |
|
0 |
(0, |
|
( |
|
|
+ |
0 |
– |
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
因此,函数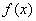 在x=
在x=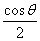 处取得极小值f (
处取得极小值f (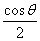 ).
).
依题意令f (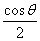 )=
)=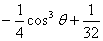 >0,0< cos
>0,0< cos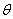 <
<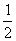 ,故
,故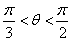 ,
,
(3)由(2)知,函数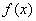 在
在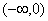 与(
与(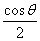 ,+
,+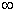 )内都是增函数。由题意,函数
)内都是增函数。由题意,函数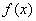 在区间(2a – 1, a)内是增函数,则a须满足:
在区间(2a – 1, a)内是增函数,则a须满足:
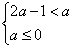 或
或
由(2)知,参数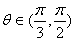 时,0< cos
时,0< cos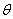 <
<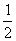 。
。
要使不等式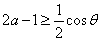 关于参数
关于参数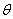 恒成立,必有
恒成立,必有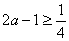 ,
,
综上解得a≤0或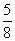 ≤a<1.
≤a<1.
故实数a的取值范围是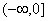 ∪
∪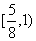


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
| 1 |
| 32 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 32 |
查看答案和解析>>
科目:高中数学 来源:黑龙江鸡西市一中2012届高三第三次月考数学文科试题 题型:013
已知函数![]() 其中x∈R,则下列结论中正确的是
其中x∈R,则下列结论中正确的是
A.f(x)是最小正周期为π的偶函数
B.f(x)的一条对称轴是![]()
C.f(x)的最大值为2
D.将![]() 向左平移
向左平移![]() 个单位得到函数f(x)的图象
个单位得到函数f(x)的图象
查看答案和解析>>
科目:高中数学 来源:荆门市2008届高三第一轮复习三角函数单元测试卷 题型:044
已知函数![]() 其中x∈R,
其中x∈R,![]() 为参数,且
为参数,且![]()
(1)当cos![]() =0时,判断函数f(x)是否有极值;
=0时,判断函数f(x)是否有极值;
(2)要使函数f(x)的极小值大于零,求参数![]() 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数![]() ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com