练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知四边形ABCD为平行四边形，A（-1，2），B（0，0），C（1，7），则点D的坐标是（　　）
    A．（-9，9）B．（-9，0）C．（0，9）D．（0，-9）

    分析 设D的坐标为（x，y），根据向量的坐标运算求出，$\overrightarrow{AB}$=（1，-2），$\overrightarrow{DC}$=（1-x，7-y），再根据$\overrightarrow{AB}$=$\overrightarrow{CD}$，即可求出x，y的值．

    解答 解：设D的坐标为（x，y），
    ∵A（-1，2），B（0，0），C（1，7），
    ∴$\overrightarrow{AB}$=（1，-2），$\overrightarrow{DC}$=（1-x，7-y），
    ∵四边形ABCD为平行四边形，
    ∴$\overrightarrow{AB}$=$\overrightarrow{CD}$，
    ∴1-x=1，7-y=-2，
    解得x=0，y=9，
    故选：C．

    点评 本题考查向量的坐标表示，属于基础题

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．4个不同的球，4个不同的盒子，把所有的球放入盒子内，求
    （1）共有多少种不同的放法？
    （2）每个盒子都不空的放法数？
    （3）恰有1个盒子不放球，共有几种放法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．为了测得河对岸塔AB的高度，先在河岸上选一点C，使C在塔底B的正东方向上，此时测得塔顶A的仰角为60°．再由点C沿北偏东15°方向走了20米到达点D，测得∠BDC=45°，则塔AB的高度为（　　）
    A．20$\sqrt{6}$米B．20$\sqrt{3}$米C．20$\sqrt{2}$米D．20米

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

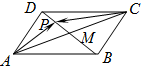    13．如图，平行四边形ABCD的两条对角线相交于点M，点P是MD中点，若|$\overrightarrow{AB}$|=2，|$\overrightarrow{AD}$|=1，且∠BAD=60°，则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为（　　）
    A．-$\frac{5}{16}$B．-$\frac{15}{16}$C．-$\frac{25}{16}$D．-$\frac{27}{16}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．曲线x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{5}x}\\{y′=\frac{1}{3}y}\end{array}\right.$后，变成的曲线方程是（　　）
    A．25x2+9y2=1B．9x2+25y2=1C．25x+9y=1D．$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知正四面体ABCD的棱长为1，求：
    （1）该四面体的内切球的表面积；
    （2）与该四面体各条棱均相切的球的体积；
    （3）该四面体的外接球上AB两点间的球面距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若sinx+siny=$\frac{1}{3}$，则t=sinx-cos2y的最大值为$\frac{4}{9}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

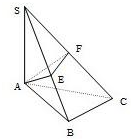    14．如图，已知SA⊥平面ABC，AB⊥BC，过点A作SB的垂线，垂足为E，过E作SC的垂线，垂足为F
    （1）求证：AE⊥平面SBC；
    （2）求证：SC⊥AF；
    （3）判断直线BC是否平行于平面AEF，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．如图所示，是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯，一个底面直径为12cm，高为8cm的圆锥形铅锤完全浸没在水中．
    （1）求该铅锤的侧面积；
    （2）当铅锤从水中取出后，杯里的水将下降多少？

    查看答案和解析>>

    同步练习册答案