
已知函数 ,其中
,其中 为正常数.
为正常数.
(Ⅰ)求函数 在
在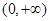 上的最大值;
上的最大值;
(Ⅱ)设数列 满足:
满足: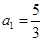 ,
, ,
,
(1)求数列 的通项公式
的通项公式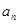 ;
;
(2)证明:对任意的 ,
, ;
;
(Ⅲ)证明: .
.
(1)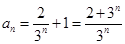
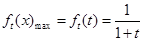
(2)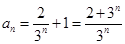 ,并运用数列的通项公式来结合函数的性质来得到证明。
,并运用数列的通项公式来结合函数的性质来得到证明。
(3)从已经研究出的性质出发,实现求和结构的放缩.
【解析】
21. 试题分析:解:(Ⅰ)由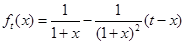 ,可得
,可得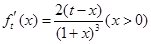 ,
,
(2 分)
所以,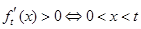 ,
,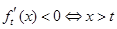 , (3 分)
, (3 分)
则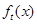 在区间
在区间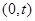 上单调递增,在区间
上单调递增,在区间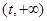 上单调递减,
上单调递减,
所以,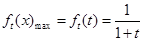 . (4 分)
. (4 分)
(Ⅱ)(1)由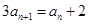 ,得
,得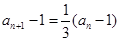 ,又
,又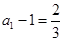 ,
,
则数列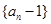 为等比数列,且
为等比数列,且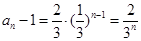 , (5 分)
, (5 分)
故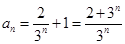 为所求通项公式. (6 分)
为所求通项公式. (6 分)
(2)即证,对任意的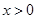 ,
, 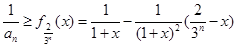
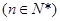
( 7分)
证法一:(从已有性质结论出发)
由(Ⅰ)知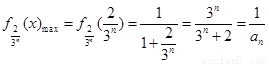 (9 分)
(9 分)
即有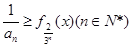 对于任意的
对于任意的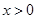 恒成立. (10 分)
恒成立. (10 分)
证法二:(作差比较法)
由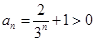 及
及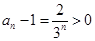 ( 8分)
( 8分)
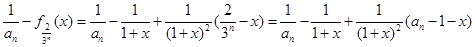
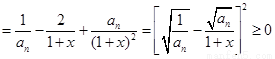 (9 分)
(9 分)
即有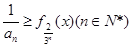 对于任意的
对于任意的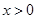 恒成立. (10 分)
恒成立. (10 分)
(Ⅲ)证法一:(从已经研究出的性质出发,实现求和结构的放缩)
由(Ⅱ)知,对于任意的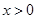 都有
都有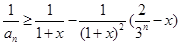 ,
,
于是,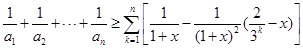
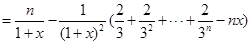
(11 分)对于任意的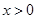 恒成立
恒成立
特别地,令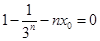 ,即
,即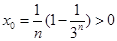 , (12 分)
, (12 分)
有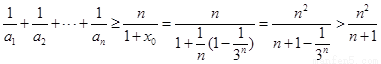 ,故原不等式成立.
,故原不等式成立.
(14 分)
以下证明小组讨论给分
证法二:(应用柯西不等式实现结构放缩)
由柯西不等式: 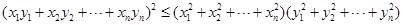
其中等号当且仅当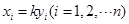 时成立.
时成立.
令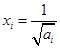 ,
,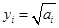 ,可得
,可得
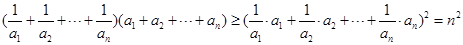
则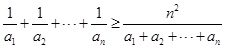
而由 ,所以
,所以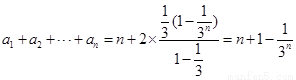
故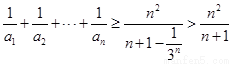 ,所证不等式成立.
,所证不等式成立.
证法三:(应用均值不等式“算术平均数”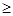 “几何平均数”)
“几何平均数”)
由均值不等式: ,其中
,其中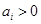
可得 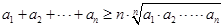 ,
, 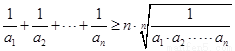
两式相乘即得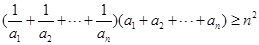 ,以下同证法二.
,以下同证法二.
证法四:(逆向分析所证不等式的结构特征,寻找证明思路)
欲证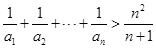 ,
,
注意到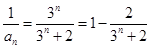 ,而
,而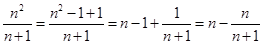
从而所证不等式可以转化为证明
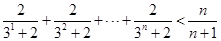
在此基础上可以考虑用数学归纳法证明此命题
考点:数列的运用
点评:本试题考查了数列的通项公式和数列的最值的运用,属于基础题。


科目:高中数学 来源: 题型:
| 1 |
| 9 |
| lim |
| n→∞ |
| x2 |
| 9 |
| y2 |
| 4 |
| 1 |
| x |
| 1 |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 ),在一次正常的试验中,取1000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有3个.
),在一次正常的试验中,取1000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有3个. Pn=0
Pn=0 -
- =1有且只有一个公共点,则这样的直线有2条.
=1有且只有一个公共点,则这样的直线有2条. +a2,g(x)=x3-a3+2a+1,若存在x1,x2∈[
+a2,g(x)=x3-a3+2a+1,若存在x1,x2∈[ ,a](a>1),使得|f(x1)-g(x2)|≤9,则a的取值范围是(1,4].
,a](a>1),使得|f(x1)-g(x2)|≤9,则a的取值范围是(1,4].查看答案和解析>>
科目:高中数学 来源:四川省同步题 题型:填空题
 ),在一次正常的试验中,取1000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有3个.
),在一次正常的试验中,取1000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有3个. Pn=0
Pn=0 ﹣
﹣ =1有且只有一个公共点,则这样的直线有2条.
=1有且只有一个公共点,则这样的直线有2条. +a2,g(x)=x3﹣a3+2a+1,若存在x1,x2∈[
+a2,g(x)=x3﹣a3+2a+1,若存在x1,x2∈[ ,a](a>1),
,a](a>1),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com