
分析 先将y=$\frac{cosx}{2-sinx}$化成cosx-ysinx=2y,再利用三角函数的和角公式化成:$\sqrt{1+{y}^{2}}$cos(x+θ)=2y,最后利用三角函数的有界性即可求得值域.
解答 解:∵y=$\frac{cosx}{2-sinx}$,
∴ysinx-2y=cosx,
∴cosx-ysinx=2y,
即:$\sqrt{1+{y}^{2}}$cos(x+θ)=2y,
∵-$\sqrt{1+{y}^{2}}$≤$\sqrt{1+{y}^{2}}$cos(x+θ)≤$\sqrt{1+{y}^{2}}$,
∴-$\sqrt{1+{y}^{2}}$≤2y≤$\sqrt{1+{y}^{2}}$,
解得:y∈[-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$].
故答案为:$[-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}]$.
点评 本题以三角函数为载体考查分式函数的值域,属于求三角函数的最值问题,属于中档题.


科目:高中数学 来源: 题型:解答题
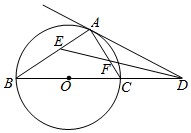 如图,已知D点在⊙O直径BC的延长线上,DA切⊙O于A点,DE是∠ADB的平分线,交AC于F点,交AB于E点.
如图,已知D点在⊙O直径BC的延长线上,DA切⊙O于A点,DE是∠ADB的平分线,交AC于F点,交AB于E点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
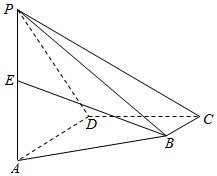 如图,四棱锥P-ABCD的底面是直角梯形,AD∥BC,∠ADC=90°,AD=2BC,PA⊥平面ABCD.
如图,四棱锥P-ABCD的底面是直角梯形,AD∥BC,∠ADC=90°,AD=2BC,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 125 | C. | 130 | D. | 135 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
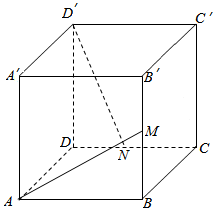 如图,在正方体ABCD-A′B′C′D′中,M、N分别是BB′,CD的中点,则异面直线AM与D′N所成的角是( )
如图,在正方体ABCD-A′B′C′D′中,M、N分别是BB′,CD的中点,则异面直线AM与D′N所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com