
 时,分别给出下面几个结论:
时,分别给出下面几个结论: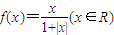 是奇函数,所以f(-x)+f(x)=0对x∈R恒成立;②可以定义证明f(x)为单调递增函数,所以f(x1)≠f(x2),则一定有x1≠x2成立;③因为f(x)为单调递增函数,所以方程|f(x)|=m不可能有两个不等的实数根;④可以判断g(x)为奇函数,并且g(x)在(-∞,0)上单调递减,即g(x)在(-∞,0)上g(x)>0,在(0,+∞)上单调递减,即g(x)在(0,+∞)上g(x)<0,故函数g(x)=f(x)-x在R上只有一个零点.
是奇函数,所以f(-x)+f(x)=0对x∈R恒成立;②可以定义证明f(x)为单调递增函数,所以f(x1)≠f(x2),则一定有x1≠x2成立;③因为f(x)为单调递增函数,所以方程|f(x)|=m不可能有两个不等的实数根;④可以判断g(x)为奇函数,并且g(x)在(-∞,0)上单调递减,即g(x)在(-∞,0)上g(x)>0,在(0,+∞)上单调递减,即g(x)在(0,+∞)上g(x)<0,故函数g(x)=f(x)-x在R上只有一个零点.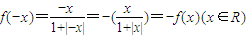 ,所以
,所以 是奇函数,故f(-x)+f(x)=0对x∈R恒成立,即①正确;
是奇函数,故f(-x)+f(x)=0对x∈R恒成立,即①正确;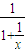 反比例函数的单调性可知,f(x)在(0,+∞)上是增函数
反比例函数的单调性可知,f(x)在(0,+∞)上是增函数

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源:2010-2011学年浙江省瑞安中学高二下学期期末试题数学文 题型:填空题
某同学在研究函数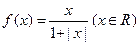 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式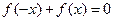 对
对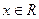 恒成立;
恒成立;
②函数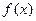 的值域为
的值域为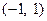 ;
;
③若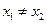 ,则一定有
,则一定有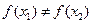 ;
;
④函数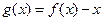 在
在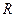 上有三个零点.
上有三个零点.
其中正确结论的序号有________________(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省无为县四高三考理科数学试卷(解析版) 题型:填空题
某同学在研究函数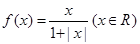 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式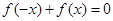 对
对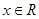 恒成立; ②函数
恒成立; ②函数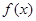 的值域为
的值域为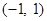 ;
;
③若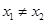 ,则一定有
,则一定有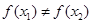 ; ④函数
; ④函数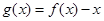 在
在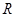 上有三个零点。 其中正确结论的序号有____________.
上有三个零点。 其中正确结论的序号有____________.
查看答案和解析>>
科目:高中数学 来源:2011年山西省高一2月月考数学试卷 题型:填空题
.某同学在研究函数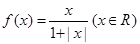 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式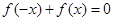 对
对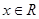 恒成立; ②函数
恒成立; ②函数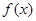 的值域为
的值域为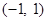 ;
;
③若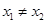 ,则一定有
,则一定有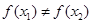 ; ④函数
; ④函数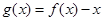 在
在 上有三个零点。
上有三个零点。
其中正确结论的序号有____ _____。(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2012届浙江省高二下学期期末试题数学文 题型:填空题
某同学在研究函数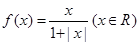 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式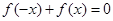 对
对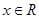 恒成立;
恒成立;
②函数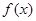 的值域为
的值域为 ;
;
③若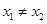 ,则一定有
,则一定有 ;
;
④函数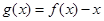 在
在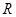 上有三个零点.
上有三个零点.
其中正确结论的序号有________________(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2012年黑龙江省高考数学仿真模拟试卷3(文科)(解析版) 题型:解答题
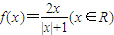 时,分别得出如下几个结论:
时,分别得出如下几个结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com