
【题目】已知α∈[0,π),在直角坐标系xOy中,直线l1的参数方程为 ![]() (t为参数);在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l2的极坐标方程是ρcos(θ﹣α)=2sin(α+
(t为参数);在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l2的极坐标方程是ρcos(θ﹣α)=2sin(α+ ![]() ).
).
(Ⅰ)求证:l1⊥l2
(Ⅱ)设点A的极坐标为(2, ![]() ),P为直线l1 , l2的交点,求|OP||AP|的最大值.
),P为直线l1 , l2的交点,求|OP||AP|的最大值.
【答案】解:(Ⅰ)证明:直线l1的参数方程为 ![]() (t为参数);
(t为参数);
消去参数t可得:直线l1的普通方程为:xsinα﹣ycosα=0.
又直线l2的极坐标方程是ρcos(θ﹣α)=2sin(α+ ![]() ).展开为ρcosθcosα+ρsinθsinα=2sin(α+
).展开为ρcosθcosα+ρsinθsinα=2sin(α+ ![]() ).
).
即直线l2的直角坐标方程为:xcosα+ysinα﹣2sin(α+ ![]() )=0.
)=0.
因为sinαcosα+(﹣cosα)sinα=0,
根据两直线垂直的条件可知,l1⊥l2.
(Ⅱ)当ρ=2, ![]() 时,ρcos(θ﹣α)=2cos
时,ρcos(θ﹣α)=2cos ![]() =2sin(α+
=2sin(α+ ![]() ).
).
所以点A(2, ![]() ),在直线ρcos(θ﹣α)=2sin(α+
),在直线ρcos(θ﹣α)=2sin(α+ ![]() )上.
)上.
设点P到直线OA的距离为d,由l1⊥l2可知,d的最大值为 ![]() =1.
=1.
于是|OP||AP|=d|OA|=2d≤2
所以|OP||AP|的最大值为2
【解析】(Ⅰ)直线l1的参数方程为 ![]() (t为参数);消去参数t可得:直线l1的普通方程.又直线l2的极坐标方程是ρcos(θ﹣α)=2sin(α+
(t为参数);消去参数t可得:直线l1的普通方程.又直线l2的极坐标方程是ρcos(θ﹣α)=2sin(α+ ![]() ).展开为ρcosθcosα+ρsinθsinα=2sin(α+
).展开为ρcosθcosα+ρsinθsinα=2sin(α+ ![]() ).利用互化公式可得直线l2的直角坐标方程,根据两直线垂直的条件即可证明:l1⊥l2.(Ⅱ)当ρ=2,
).利用互化公式可得直线l2的直角坐标方程,根据两直线垂直的条件即可证明:l1⊥l2.(Ⅱ)当ρ=2, ![]() 时,满足方程ρcos(θ﹣α)=2sin(α+
时,满足方程ρcos(θ﹣α)=2sin(α+ ![]() ).可得点A(2,
).可得点A(2, ![]() ),在直线ρcos(θ﹣α)=2sin(α+
),在直线ρcos(θ﹣α)=2sin(α+ ![]() )上.设点P到直线OA的距离为d,由l1⊥l2可知,d的最大值为
)上.设点P到直线OA的距离为d,由l1⊥l2可知,d的最大值为 ![]() =1.即可得出|OP||AP|=d|OA|=2d最大值.
=1.即可得出|OP||AP|=d|OA|=2d最大值.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆方程为 ![]() +y2=1,圆C:(x﹣1)2+y2=r2 .
+y2=1,圆C:(x﹣1)2+y2=r2 . 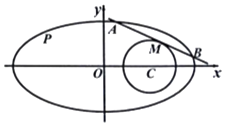
(Ⅰ)求椭圆上动点P与圆心C距离的最小值;
(Ⅱ)如图,直线l与椭圆相交于A、B两点,且与圆C相切于点M,若满足M为线段AB中点的直线l有4条,求半径r的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点E(﹣2,0),点P时圆F:(x﹣2)2+y2=36上任意一点,线段EP的垂直平分线交FP于点M,点M的轨迹记为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)过F的直线交曲线C于不同的A、B两点,交y轴于点N,已知 ![]() =m
=m ![]() ,
, ![]() =n
=n ![]() ,求m+n的值.
,求m+n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( ) 
A.100πcm3
B.![]()
C.400πcm3
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a2=2,其前n项和Sn满足: ![]() (n∈N*).
(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为  (其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4cosθ.
(其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4cosθ.
(Ⅰ)写出直线l和曲线C的普通方程;
(Ⅱ)已知点P为曲线C上的动点,求P到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明1+2+3+…+n2= ![]() ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.k2+1
B.(k+1)2
C.![]()
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁. 
(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
网购迷 | 非网购迷 | 合计 | |
年龄不超过40岁 | |||
年龄超过40岁 | |||
合计 |
(2)若从网购迷中任意选取2名,求其中年龄丑啊过40岁的市民人数ξ的分布列与期望. 附: ![]() ;
;
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com