
 某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为 .
某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为 .  ,而所求事件“该部件的使用寿命超过1000小时”当且仅当“超过1000小时时,元件1、元件2至少有一个正常”和“超过1000小时时,元件3正常”同时发生,由于其为独立事件,故分别求其概率再相乘即可
,而所求事件“该部件的使用寿命超过1000小时”当且仅当“超过1000小时时,元件1、元件2至少有一个正常”和“超过1000小时时,元件3正常”同时发生,由于其为独立事件,故分别求其概率再相乘即可
 ,P(B)=
,P(B)=
 ×
× =
=



科目:高中数学 来源: 题型:
 (2012•黑龙江)某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为
(2012•黑龙江)某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为| 3 |
| 8 |
| 3 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
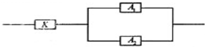 如图,某个部件由三个元件按如图方式连接而成,元件K正常工作且元件
如图,某个部件由三个元件按如图方式连接而成,元件K正常工作且元件| A、0.19 | B、0.019 | C、0.01 | D、0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012新课标理)某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从
正态分布![]() ,且各个元件能否正常相互独立,那么该部件的使用寿命
,且各个元件能否正常相互独立,那么该部件的使用寿命
 超过1000小时的概率为_________
超过1000小时的概率为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布![]() ,且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为
,且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com