
分析 (1)先求导,再由函数f(x)没有极值,得到函数单调递增或单调递减,问题得以解决,
(2)由函数f(x)在区间(2,3)上单调递减,得到f′(2)≤0且f′(3)≤0,即可求出a的范围.
解答 解:(1)$f'(x)=6{x^2}-6({a+\frac{1}{a}})x+6=6({x-a})(x-\frac{1}{a})$,
由条件,只需${[{6({a+\frac{1}{a}})}]^2}-4×6×6≤0$,
即${(a+\frac{1}{a})^2}≤0$,
所以$a=\frac{1}{a}$,
因为a>0,
从而a=1.
(2)由条件,知f′(2)≤0且f′(3)≤0,
即$\left\{\begin{array}{l}{(2-a)(2-\frac{1}{a})≤0}\\{(3-a)(3-\frac{1}{a})≤0}\end{array}\right.$,
因为a>0,
所以$\left\{\begin{array}{l}{(a-2)(2a-1)≥0}\\{(a-3)(3a-1)≥0}\end{array}\right.$,
解得a≤$\frac{1}{3}$或a≥3
点评 本题考查函数的导数的应用以及参数的取值范围,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
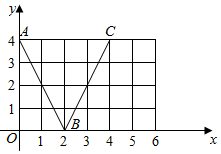 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4),则$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4),则$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | $[\frac{{\sqrt{2}}}{2},+∞)$ | C. | $[{\frac{{\sqrt{2}}}{4},+∞})$ | D. | $[\sqrt{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com