
【题目】如图,AB是⊙O的直径,P是⊙O所在平面外一点,PA垂直于⊙O所在平面,且PA=AB=10,设点C为⊙O上异于A、B的任意一点. 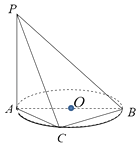
(1)求证:BC⊥平面PAC;
(2)若AC=6,求三棱锥C﹣PAB的体积.
【答案】
(1)证明:∵AB是⊙O的直径,点C为⊙O上异于A、B的任意一点,
∴AC⊥BC,
∵P是⊙O所在平面外一点,PA垂直于⊙O所在平面,BC⊙O所在平面,
∴BC⊥PA,
∵AC∩PA=A,
∴BC⊥平面PAC
(2)解:∵AC=6,PA=AB=10,
∴BC= ![]() =8,
=8,
∵PA垂直于⊙O所在平面,∴PA⊥平面ABC,
又PA平面PAB,∴平面PAB⊥平面ABC,
∴点C到AB的距离d即为点C到平面PAB的距离,
∵ ![]() =
= ![]() ,
,
∴d= ![]() =
= ![]() =
= ![]() ,
,
又S△PAB= ![]() =50,
=50,
∴三棱锥C﹣PAB的体积V= ![]() =
= ![]() =80
=80
【解析】(1)由圆的性质得AC⊥BC,由线面垂直得BC⊥PA,由此能证明BC⊥平面PAC.(2)由勾股和得BC=8,推导出平面PAB⊥平面ABC,从而点C到AB的距离d即为点C到平面PAB的距离,由此能求出三棱锥C﹣PAB的体积.
【考点精析】利用直线与平面垂直的判定对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆锥曲线 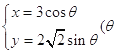 为参数)和定点
为参数)和定点 ![]() F1 , F2是圆锥曲线的左右焦点。
F1 , F2是圆锥曲线的左右焦点。
(1)求经过点F2且垂直于直线AF1的直线l的参数方程;
(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(3x+ ![]() )的图象,只需要把函数y=sin(x+
)的图象,只需要把函数y=sin(x+ ![]() )的图象上的所有点( )
)的图象上的所有点( )
A.横坐标伸长为原来的3倍,纵坐标不变
B.横坐标缩短为原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
C.纵坐标伸长为原来的3倍,横坐标不变
D.纵坐标缩短为原来的 ![]() 倍,横坐标不变
倍,横坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km). 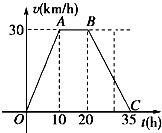
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】工人在安装一个正六边形零件时,需要固定如图所示的六个位置的螺丝,第一阶段,首先随意拧一个螺丝,接着拧它对角线上(距离它最远的,下同)螺丝,再随意拧第三个螺丝,第四个也拧它对角线上螺丝,第五个和第六个以此类推,但每个螺丝都不要拧死;第二阶段,将每个螺丝拧死,但不能连续拧相邻的2个螺丝。则不同的固定方式有 . 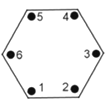
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ka﹣x(k,a为常数,a>0且a≠1)的图象过点A(0,1),B(3,8).
(1)求函数f(x)的解析式;
(2)若函数g(x)= ![]() 是奇函数,求b的值;
是奇函数,求b的值;
(3)在(2)的条件下判断函数g(x)的单调性,并用定义证明你的结论;
(4)解不等式g(3x)+g(x﹣3﹣x2)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com