Question

（04全国卷I）（12分）

如图，已知四棱锥 P―ABCD，PB⊥AD侧面PAD为边长等于2的正三角形，底面ABCD为菱形，侧面PAD与底面ABCD所成的二面角为120°.

（I）求点P到平面ABCD的距离，

（II）求面APB与面CPB所成二面角的大小.

 

 

 

 

 

 

 

 

Answer 1

解析：（I）如图，作PO⊥平面ABCD，垂足为点O.连结OB、OA、OD、OB与AD交于点E，连结PE.

∵AD⊥PB，∴AD⊥OB，

∵PA=PD，∴OA=OD，

于是OB平分AD，点E为AD的中点，所以PE⊥AD.

由此知∠PEB为面PAD与面ABCD所成二面角的平面角，

∴∠PEB=120°，∠PEO=60°

由已知可求得PE=

∴PO=PE?sin60°=，

即点P到平面ABCD的距离为.

（II）解法一：如图建立直角坐标系，其中O为坐标原点，x轴平行于DA.

.连结AG.

又知由此得到：

所以

等于所求二面角的平面角，

于是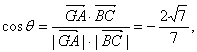

所以所求二面角的大小为  .

解法二：如图，取PB的中点G，PC的中点F，连结EG、AG、GF，则AG⊥PB，FG//BC，FG=BC.

∵AD⊥PB，∴BC⊥PB，FG⊥PB，

∴∠AGF是所求二面角的平面角.

∵AD⊥面POB，∴AD⊥EG.

又∵PE=BE，∴EG⊥PB，且∠PEG=60°.

在Rt△PEG中，EG=PE?cos60°=.

在Rt△PEG中，EG=AD=1.

于是tan∠GAE==,

又∠AGF=π－∠GAE.

所以所求二面角的大小为π－arctan.