
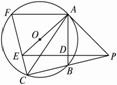
图12
(1)求证:PD·PE =PB·PC;
(2)求证:PE∥AF;
(3)连结AC,若AE∶AC=1∶![]() ,AB=2,求EF的长.
,AB=2,求EF的长.
思路分析:(1)证明等积式往往考虑相似三角形,但△PBD与△PEC不相似,因此要用PA2=PB·PC进行等积变换.?
(2)要证明PE∥AF,只需证明同位角∠PEC和∠F相等.?
(3)首先找出EF与AB的关系,同时注意到AE∶AC=1∶![]() ,因此,先设法求出EF∶AB,这可由相似三角形得出.
,因此,先设法求出EF∶AB,这可由相似三角形得出.
(1)证明:∵PA切⊙O于A,?
∴PA2=PB·PC,PA⊥AE.?
又AD⊥PE,∴△APE∽△DPA.?
∴PA2=PD·PE.∴PD·PE =PB·PC.
(2)证明:∵PD·PE =PB·PC,∴![]() =
=![]() .?
.?
又∠EPC =∠BPD,∴△BPD∽△EPC.?
∴∠PBD =∠PEC.又∵∠PBD =∠F,?
∴∠PEC =∠F.∴PE∥AF.
(3)解:∵PA切⊙O于A,∴∠BAP =∠ACP.?
∵∠APB =∠CPA,∴△APB∽△CPA.?
∴![]() =
=![]() .?
.?
又∵∠ABP =∠F,∠BAP =∠AEP =∠FAE,?
∴△AEF∽△APB.∴![]() =
=![]() .?
.?
∴![]() =
=![]() .∴
.∴![]() =
=![]() =
=![]() .?
.?
又AB =2,∴![]() .
.


科目:高中数学 来源: 题型:
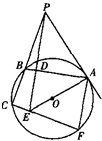 如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
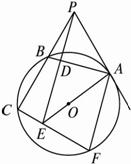
图2-5-6
(1)求证:△PBD∽△PEC;
(2)若AB=12,tan∠EAF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二下学期三调理科数学试卷(解析版) 题型:解答题
(本题满分12分)
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C, 于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。

(1)求证:B,C,E,D四点共圆;
(2)当AB=12, 时,求圆O的半径.
时,求圆O的半径.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省衡水中学高二(下)三调数学试卷(理科)(解析版) 题型:解答题
 时,求圆O的半径.
时,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com