【题目】偶函数 
= 
的图象过点 
,且在 
处的切线方程为 
.求 
的解析式．
【答案】
【解析】解：∵f(x)为偶函数,
∴b＝d＝0.
又图象过点P(0,1),则e＝1.
此时f(x)＝ax4＋cx2＋1.
∴y′＝4ax3＋2cx,
∴y′|x＝1＝4a＋2c＝1. ①
又切线的切点(1,-1)在曲线上,
∴a＋c＋1＝-1. ②
由①②得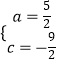 
,
∴f(x) ＝ 
x4- 
x2＋1.
所以答案是：
.
【考点精析】本题主要考查了函数的偶函数和导数的几何意义的相关知识点，需要掌握一般地，对于函数f(x)的定义域内的任意一个x，都有f(－x)=f(x)，那么f(x)就叫做偶函数；通过图像,我们可以看出当点
趋近于
时，直线
与曲线相切．容易知道，割线
的斜率是
，当点趋近于时，函数
在
处的导数就是切线PT的斜率k，即
才能正确解答此题．
科目：高中数学 来源： 题型：
【题目】已知数列{an}满足：a1=1，|an+1－an|=pn，n∈N*，Sn为数列{an}的前n项和.
（1）若{an}是递增数列，且a1，2a2，3a3成等差数列，求p的值；
（2）若p=
，且{a2n－1}是递增数列，{a2n}是递减数列，求数列{an}的通项公式；
（3）在（2）的条件下，令cn=n（an+1－an），求数列{cn}的前n项和Tn.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知矩形ABCD中，E、F分别是AB、CD上的点，BE=CF=1，BC=2，AB=CD=3，P、Q分别为DE、CF的中点，现沿着EF翻折，使得二面角A﹣EF﹣B大小为 
．
（Ⅰ）求证：PQ∥平面BCD；
（Ⅱ）求二面角A﹣DB﹣E的余弦值．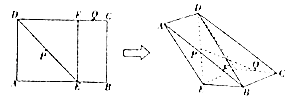
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】过 
轴上动点 
引抛物线 
的两条切线 
、 
， 
、 
为切点，设切线 、 的斜率分别为 
和 
.
（Ⅰ）求证： 
；
（Ⅱ）求证：直线 
恒过定点，并求出此定点坐标；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知△ABC的面积为3，且满足0≤
≤6，设
与
的夹角为θ.
(1)求θ的取值范围；
(2)求函数f(θ)＝2sin2
－
(cos θ＋sin θ)·(cos θ－sin θ)的最大值与最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆 
的中心在原点焦点在 
轴上，离心率等于 
，它的一个顶点恰好是抛物线 
的焦点.
（1）求椭圆 的焦点；
（2）已知点 
在椭圆 上，点 
是椭圆 上不同于 
的两个动点，且满足： 
，试问：直线 
的斜率是否为定值？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定点 
， 
为圆 
上任意一点，线段 
上一点 
满足 
，直线 
上一点 
，满足 
.
（1）当 在圆周上运动时，求点 
的轨迹 
的方程；
（2）若直线 
与曲线 交于 
两点，且以 
为直径的圆过原点 
，求证：直线 与 
不可能相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
