现有8名语、数、外成绩优秀者,其中A1,A2,A3语文成绩优秀,B1,B2,B3数学成绩优秀,C1,C2外语成绩优秀,从中选出语、数、外成绩优秀者各1名,组成一个小组代表学校参加竞赛.
(1)求C1被选中的概率.
(2)求A1和B1同时被选中的概率.
【答案】
分析:(1)从3个语文成绩优秀者,2个数学成绩优秀者,2名外语成绩优秀者各选一个人,共有3×3×2=18种方法,满足条件的有3×3种结果,代入公式,得到结果.
(2)A
1和B
1同时被选中的这一事件,共有2种结果代入公式,得到结果.
解答:解:(Ⅰ)从7人中选出数学、物理、化学成绩优秀者各1名,其一切可能的结果组成的基本事件Ω={(A
1,B
1,C
1),(A
1,B
1,C
2),(A
1,B
2,C
1),(A
1,B
2,C
2),(A
1,B
3,C
1),(A
1,B
3,C
2),(A
2,B
1,C
1),(A
2,B
1,C
2),(A
2,B
2,C
1),(A
2,B
2,C
2),(A
2,B
3,C
1),(A
2,B
3,C
2),(A
3,B
1,C
1),(A
3,B
1,C
2),(A
3,B
2,C
1),(A
3,B
2,C
2),(A
3,B
3,C
1),(A
3,B
3,C
2).}
由12个基本事件组成.由于每一个基本事件被抽取的机会均等,因此这些基本事件的发生是等可能的,用M表示“C
1恰被选中”这一事件,则
M={(A
1,B
1,C
1),(A
1,B
2,C
1),(A
1,B
3,C
1),(A
2,B
1,C
1),(A
2,B
2,C
1),(A
2,B
3,C
1),(A
3,B
1,C
1),(A
3,B
2,C
1),(A
3,B
3,C
1)}.
事件M由6个基本事件组成,因而P(M)=
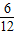
=

.
(Ⅱ)用N表示“A
1,B
1全被选中”这一事件,
由于N={(A
1,B
1,C
1),(A
1,B
1,C
2)},有2个基本事件组成.
所以P(N)=
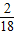
=
 点评:
点评:本题能充分体现列举法的优点,注意激发学生学习数学的情感,培养其严谨治学的态度.在学生分析问题、解决问题的过程中培养其积极探索的精神.

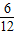 =
= .
.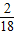 =
=


 阅读快车系列答案
阅读快车系列答案![]() 通晓日语,
通晓日语,![]() 通晓俄语,
通晓俄语,![]() 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.![]() 被选中的概率;
被选中的概率;![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.