
 (n∈N*,a,b∈R).
(n∈N*,a,b∈R). ,求a,b的值.
,求a,b的值. ,所以当a=b=1时,
,所以当a=b=1时,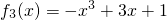
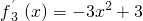 =-3(x2-1).
=-3(x2-1). ,在(1,2)内,
,在(1,2)内,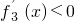 ,
,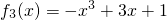 为增函数,在(1,2)内
为增函数,在(1,2)内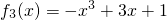 为减函数.
为减函数.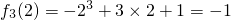 .
.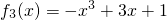 在[0,2]上的最大值为f3(1)=3,最小值为f3(2)=-1;
在[0,2]上的最大值为f3(1)=3,最小值为f3(2)=-1; .
. =-3(x2-a),
=-3(x2-a),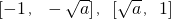 内f′3(x)0,
内f′3(x)0,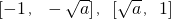 内为减函数,
内为减函数,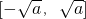 内为增函数,
内为增函数, ,则
,则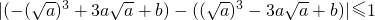
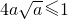 ,解得:
,解得: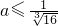 .
.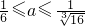 .
.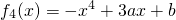 .
. ,则
,则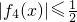 ,
,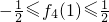 ,即
,即 ①
①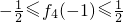 ,即
,即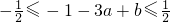 ②
②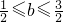 ,又因为
,又因为 ,所以
,所以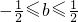 ,所以
,所以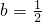 .
.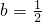 代入①得:
代入①得: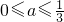 ,
,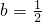 代入②得:
代入②得: ≤a≤0.
≤a≤0. .
.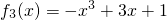 ,求导后利用导函数的零点将(0,2)分段,由单调性判出极值点,求出极值,再求出端点值,则f3(x)在[0,2]上的最大值和最小值可求;
,求导后利用导函数的零点将(0,2)分段,由单调性判出极值点,求出极值,再求出端点值,则f3(x)在[0,2]上的最大值和最小值可求;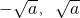 ,再求出函数f3(x)在(-1,1)上的极大值和极小值,再由极大值和极小值差的绝对值小于等于1求出a的取值范围,和由|f3(1)-f3(-1)|≤1求出的a的范围取交集即可;
,再求出函数f3(x)在(-1,1)上的极大值和极小值,再由极大值和极小值差的绝对值小于等于1求出a的取值范围,和由|f3(1)-f3(-1)|≤1求出的a的范围取交集即可; ,则x取-1和1时的函数值都在
,则x取-1和1时的函数值都在 和
和 之间,联立解出b的范围,再由x取0时的函数值也在
之间,联立解出b的范围,再由x取0时的函数值也在 和
和 之间,得到b的范围,两者结合即可求出b的值,把b的值代入x取-1和1时的式子,即可得到a的值.
之间,得到b的范围,两者结合即可求出b的值,把b的值代入x取-1和1时的式子,即可得到a的值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |
| f(x)2-2x |
| 2 |
| s2 |
| 2 |
| s3 |
| 3 |
| sn |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a+1 | x |
查看答案和解析>>
科目:高中数学 来源:2013年江苏省盐城市高考数学二模试卷(解析版) 题型:解答题
 (n∈N*,a,b∈R).
(n∈N*,a,b∈R). ,求a,b的值.
,求a,b的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com