
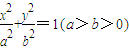 经过点(0,1),过右焦点F且不与x轴重合的动直线L交椭圆于A,C两点,当动直线L的斜率为2时,坐标原点O到L的距离为
经过点(0,1),过右焦点F且不与x轴重合的动直线L交椭圆于A,C两点,当动直线L的斜率为2时,坐标原点O到L的距离为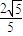 .
.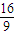 时,求直线L的方程.
时,求直线L的方程.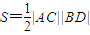 =
=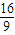 可求出k的值,确定直线L的方程.
可求出k的值,确定直线L的方程.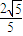 ,
,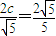 ,c=1.
,c=1.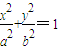 经过点(0,1),
经过点(0,1),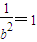 ,b=1,由a2=b2+c2得a2=2.
,b=1,由a2=b2+c2得a2=2.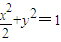
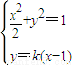 得,(2k2+1)x2-4k2x+2k2-2=0.
得,(2k2+1)x2-4k2x+2k2-2=0.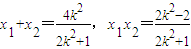 ,
,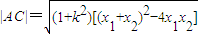 =
=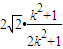 (*)
(*)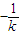 (x-1).
(x-1).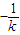 ,类比可得
,类比可得 ,
,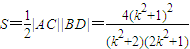 =
=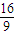 ,
,

科目:高中数学 来源:2013届湖北武汉部分重点中学(五校)高二下期中文科数学卷(解析版) 题型:解答题
(14分)已知椭圆 经过点(0,1),离心率
经过点(0,1),离心率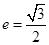 。
。
(1)求椭圆C的方程;
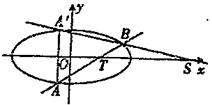
(2)设直线 与椭圆C交于A、B两点,点A关于x轴的对称点为
与椭圆C交于A、B两点,点A关于x轴的对称点为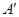 。
。
①试建立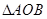 的面积关于m的函数关系;
的面积关于m的函数关系;
②某校高二(1)班数学兴趣小组通过试验操作初步推断;“当m变化时,直线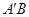 与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省高三上学期期末考试理科数学试卷 题型:解答题
已知椭圆 经过点(0,
经过点(0, ),离心率为
),离心率为 ,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且 ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求 的值是否为定值?若是,求出
的值是否为定值?若是,求出 的值,否则,说明理由;
的值,否则,说明理由;
(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三上学期期中考试数学文卷 题型:解答题
(本小题满分15分)已知椭圆 经过点(0,1),离心率
经过点(0,1),离心率
(I)求椭圆C的方程;
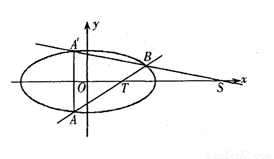
(II)设直线 与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线
与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线 与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分13分)已知椭圆![]() 经过点(0,
经过点(0,![]() ),离心率为
),离心率为![]() ,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且![]() ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求![]() 的值是否为定值?若是,求出
的值是否为定值?若是,求出![]() 的值,否则,说明理由;
的值,否则,说明理由;
(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
已知椭圆![]() 经过点(0,
经过点(0,![]() ),离心率为
),离心率为![]() ,经过椭圆C的右焦点F的直线l交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
,经过椭圆C的右焦点F的直线l交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(1)求椭圆C的方程;
(2)若直线l交y轴于点M,且![]() ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求![]() 的值是否为定值?若是,求出
的值是否为定值?若是,求出![]() 的值,否则,说明理由;
的值,否则,说明理由;
(3)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com